Implement insert and delete in a tri-nary tree. A tri-nary tree is much like a binary tree but with three child nodes for each parent instead of two -- with the left node being values less than the parent, the right node values greater than the parent, and the middle nodes values equal to the parent.
For example, suppose I added the following nodes to the tree in this order: 5, 4, 9, 5, 7, 2, 2. The resulting tree would look like this:
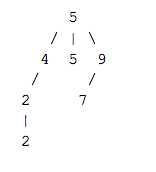
1 /* 2 * Author: Min Li 3 * This code can implement insert and delete in a tri-nary tree. 4 */ 5 6 #include<iostream> 7 8 using namespace std; 9 10 11 // Definition for Tree Node 12 struct TreeNode { 13 public: 14 int val; 15 TreeNode *left; 16 TreeNode *right; 17 TreeNode *middle; 18 TreeNode(int x) : val(x), left(NULL), right(NULL), middle(NULL) {} 19 }; 20 21 22 // Class: trinaryTree 23 class trinaryTree { 24 public: 25 TreeNode* insert(TreeNode *root, int value); // Insert a node 26 TreeNode* deleteNode(TreeNode *root, int value); // Delete a node 27 TreeNode* findSuccessor(TreeNode *root); // Find a node‘s successor 28 bool test(); // Test my code 29 }; 30 31 32 // Method: Insert a node into tri-nary tree 33 // return the root of new tri-nary tree 34 TreeNode* trinaryTree:: insert(TreeNode *root, int value) { 35 TreeNode *Node = new TreeNode(value); 36 if(root==NULL) // tree is empty 37 root = Node; 38 else { 39 TreeNode *parent; 40 TreeNode *tmpNode = root; 41 // Find the parent of "Node" 42 while(tmpNode!=NULL) { 43 parent = tmpNode; 44 if(tmpNode->val < Node->val) // Node is in the right subtree 45 tmpNode = tmpNode->right; 46 else if(tmpNode->val > Node->val) // Node is in the left subtree 47 tmpNode = tmpNode->left; 48 else // Node is in the middle subtree 49 tmpNode = tmpNode->middle; 50 } 51 // Insert the Node under parent 52 if(Node->val == parent->val) 53 parent->middle = Node; 54 else if(Node->val > parent->val) 55 parent->right = Node; 56 else 57 parent->left = Node; 58 } 59 return root; 60 } 61 62 // Method: Delete a node from tri-nary tree 63 // Return the root of new tree 64 TreeNode* trinaryTree:: deleteNode(TreeNode *root, int value) { 65 66 if(root==NULL) 67 return NULL; 68 if(root->val == value) { 69 if(root->left==NULL && root->middle==NULL && root->right==NULL) { // Delete a leaf 70 delete root; 71 return NULL; 72 } 73 if(root->middle!=NULL) { // Middle child is not empty 74 root->middle = deleteNode(root->middle,value); 75 } 76 else { 77 if(root->left==NULL) { // Left child is empty, but right child is not 78 TreeNode* rightChild = root->right; 79 delete root; 80 return rightChild; 81 82 } 83 else if(root->right==NULL) { // Right child is empty, but left child is not 84 TreeNode* leftChild = root->left; 85 delete root; 86 return leftChild; 87 } 88 else { // Both left and right child exists 89 TreeNode *successor = findSuccessor(root->right); 90 root->val = successor->val; 91 root->right = deleteNode(root->right,successor->val); 92 } 93 } 94 } 95 else if(root->val > value) // Recursive left subtree 96 root->left = deleteNode(root->left,value); 97 else // Recursive right subtree 98 root->right = deleteNode(root->right,value); 99 100 return root; 101 } 102 103 // Method: Find the successor 104 TreeNode* trinaryTree:: findSuccessor(TreeNode *root) { 105 if(root->left==NULL) 106 return root; 107 else 108 return findSuccessor(root->left); 109 } 110 111 112 // Method: Test 113 bool trinaryTree:: test() { 114 trinaryTree test; 115 TreeNode *root = NULL; 116 TreeNode *node; 117 118 // Test tree insert 119 int val[] = {5,4,9,5,7,2,2}; 120 int i; 121 for(i=0;i<sizeof(val)/sizeof(int);i++) { 122 root = test.insert(root,val[i]); 123 124 } 125 126 // Test tree delete 127 // Case1: delete a leaf 128 test.deleteNode(root,5); 129 // Case2: delete root 130 test.deleteNode(root,5); 131 // Case3: delete a node with only left child 132 test.deleteNode(root,4); 133 134 return true; 135 136 137 }
Implement Insert and Delete of Tri-nay Tree
原文:http://www.cnblogs.com/sdytlm/p/4034163.html