We‘ll call an array of n non-negative integers a[1],?a[2],?...,?a[n] interesting,
if it meets m constraints. The i-th of the m constraints
consists of three integers li, ri, qi (1?≤?li?≤?ri?≤?n)
meaning that value 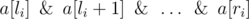 should
be equal to qi.
should
be equal to qi.
Your task is to find any interesting array of n elements or state that such array doesn‘t exist.
Expression x&y means the bitwise AND of numbers x and y. In programming languages C++, Java and Python this operation is represented as "&", in Pascal — as "and".
The first line contains two integers n, m (1?≤?n?≤?105, 1?≤?m?≤?105) — the number of elements in the array and the number of limits.
Each of the next m lines contains three integers li, ri, qi (1?≤?li?≤?ri?≤?n, 0?≤?qi?<?230) describing the i-th limit.
If the interesting array exists, in the first line print "YES" (without the quotes) and in the second line print n integers a[1],?a[2],?...,?a[n] (0?≤?a[i]?<?230) decribing the interesting array. If there are multiple answers, print any of them.
If the interesting array doesn‘t exist, print "NO" (without the quotes) in the single line.
3 1 1 3 3
YES 3 3 3
3 2 1 3 3 1 3 2
NO
假设有n个非负数,现在有m个限制,a[l] & a[l+1] & a[l+2] ... & a[r] = q。要求根据上述的限制,输出符合要求的1~n个数,如若不能则输出“NO”。
我们先挖掘题意,弄清楚题目给的已知条件和要我们输出什么。
a[l] & a[l+1] & a[l+2] ... & a[r] = q,这是每个限制的基本形式,由“&”我们可以得知,如若q中的某一个bit是1的话,则要求a[l]~a[r]中的那个bit位都为1。这个条件看似是限制,现在通过转化,似乎可以成为我们的已知条件,即每一个a[i]中的必须要为1的bit。
通过上述可知,我们得到每个a[i]的基本值,然后每一个限制是一个区间,很容易就想到了线段树,对每一条限制进行查询,看是否冲突,如若冲突则为"NO“,如若不冲突,则就按照a[i]的必须值来输出即可。
#include <cstdio>
#include <cstring>
#define Maxbit 29
#define M_max 123456
#define N_max 123456
#define root 1, 1, n
using namespace std;
const int noth = (1<<30)-1;
int n, m;
int l[M_max], r[M_max], q[M_max], a[N_max];
int sum[N_max], tree[N_max*3];
void build(int v, int l, int r) {
if (l == r) {
tree[v] = a[l];
return;
}
int ls = v<<1, rs = ls+1, mid = (l+r)>>1;
build(ls, l, mid);
build(rs, mid+1, r);
tree[v] = tree[ls] & tree[rs];
}
int query(int v, int l, int r, int ql, int qr) {
if (r < ql || l > qr) return noth;
if (ql <= l && r <= qr) return tree[v];
int ls = v<<1, rs = ls+1, mid = (l+r)>>1;
return query(ls, l, mid, ql, qr) & query(rs, mid+1, r, ql, qr);
}
void init() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
scanf("%d%d%d", &l[i], &r[i], &q[i]);
for (int i = 0; i <= Maxbit; i++) {
memset(sum, 0, sizeof(sum));
for (int j = 1; j <= m; j++)
if ((q[j] >> i) & 1) {
sum[l[j]]++;
sum[r[j]+1]--;
}
for (int j = 1; j <= n; j++) {
sum[j] += sum[j-1];
if (sum[j] > 0) a[j] |= 1 << i;
}
}
build(root);
}
void solve() {
for (int i = 1; i <= m; i++)
if (query(root, l[i], r[i]) != q[i]) {
printf("NO\n");
return;
}
printf("YES\n");
for (int i = 1; i <= n; i++) printf("%d ", a[i]);
printf("\n");
}
int main() {
init();
solve();
}codeforces Round #275(div2) D解题报告
原文:http://blog.csdn.net/lmhunter/article/details/40514911