由于第一次实验的实验报告不在这台机器,先写这一算法吧。
SGDLR(the Stochastic Gradient Descent for Logistic Regression),要讲解这一算法,首先要把名字拆为几块。
1 随机 2 梯度下降 3逻辑回归
先贴一篇文章:http://blog.csdn.net/zouxy09/article/details/20319673
这篇文章中解释的还不错。
其实这一算法,通俗来讲是这样子的:
1、手中肯定有很多带有label标记的数据,这是训练集。
2、我们期望能够建立一个带参数的式子,来计算某种情况出现的概率,以便于后面预测测试集的类别的时候,计算它在每一类的概率,取概率大的为自己的类。
3、由于sigmoid函数的优势:连续,光滑,严格单调,关于(0,0.5)中心对称,形如下图,

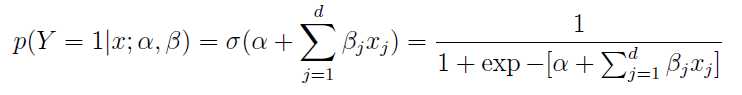 公式①
公式①
利用下面这个式子变换得到:
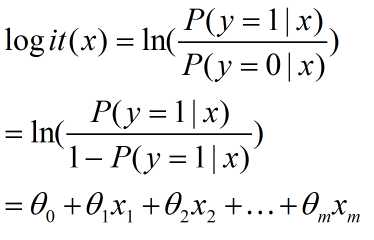
所以我们只需要计算出参数的值,就可以用公式①计算概率。
4、所有在训练集中出现的样本,已经真实存在了,所以它们带入计算出的概率应该是最大的,理想情况为1。根据这一特征来计算参数值。
5、式子并不是一个线性可解的,需要使用极大似然,这一算法不再赘述请自行谷歌。但是后来发现求参数的偏导数的时候,导数为0线性不可解,这时候就要用到梯度下降的算法。
6、所谓梯度下降的算法,事实上是从一个起点,一步步的试探,来回震荡,直到找到一个最低点。迭代公式如下:(这里的lamda是步长,自己设定,参数的初值也是自己设定)
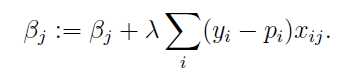
普通的梯度下降需要每次都用所有样本加和,然后迭代到收敛。
7、那么随机梯度下降就是在普通的情况下,每次只迭代一个样本(注意:这个样本必须是随机抽的,如果有偏向,最后的结果会很难看),直到收敛。
8、利用以上的迭代公式可以得到参数的值。
9、如果存在多个分类,那么可以训练多个分类器,一类一个,每一个训练样本都只属于下面两类:“是这类”和“不是这类”。训练的时候也是训练N套参数。
对于一个测试样本,带入每一个分类器计算一遍概率,以概率最大的分类有效。
该算法依旧可以使用十次交叉验证检验效果。
原文:http://www.cnblogs.com/lilylee/p/4065838.html