难得的中文题,就不翻译了。
输入第一行为T,表示有T组测试数据。
每组数据以两个整数N和M开始,表示地图的规模。接下来的N行,每一行包含一个长度为M的字符串,表示地图,‘.’表示陆地,’E’表示浅海域,’D’表示深海域。
[Technical Specification]
1. 1 <= T <= 100
2. 1 <= N, M <= 47
题意:假设地图为一个N*M的格子,其中一些是陆地,一些是可以填充的浅海域,一些是不可填充的深海域。这里定义海岸线的长度为一个联通块陆地(可能包含浅海域填充变为的陆地)的边缘长度,两个格子至少有一个公共边,则视为联通。
值得注意的是,这里Z市的陆地区域可以是不联通的,并且整个地图都处在海洋之中,也就是说,Z市是由一些孤岛组成的,比如像,夏威夷?
你的任务是,填充某些浅海域,使得所有岛屿的海岸线之和最长。
输出最长海岸线和。
Solution:
一开始以为是贪心,后来发现这个规划问题好像不可以。算法是最小割,然后最小割==最大流,算法是最大流。
由于海岸线一定是海与岸的边界(废话哈哈哈~~~),不妨在给出的网格图外层加多层深海(的孤独~~~)
显然(i+j)%2==0的格子只可能和(i+j)%2==1的格子有海岸线。不妨二部图。
我们需要求的是最可能多的相邻不同对(<‘D‘, ‘.‘>),也就是求尽可能少的相邻相同对(<‘D‘, ‘D‘>或<‘.‘, ‘.‘>)。
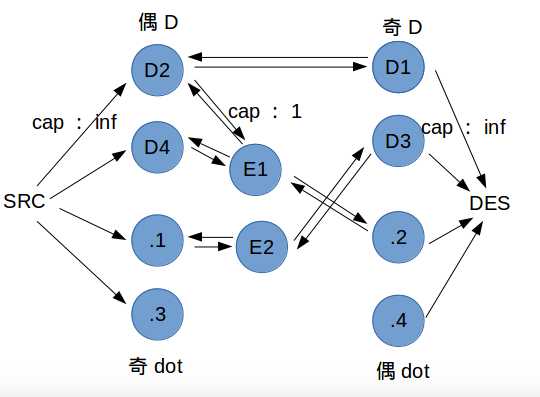
建模如图,感觉这样画图比较直观。只画出部分,还有EE相连之类的。
左右流量均为inf,中间流量为1。
显然最大流跑出来的是最少的相同对数。
答案就是 sum - mf
#pragma comment (linker,"/STACK:102400000,102400000")
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#include <stack>
using namespace std;
#define mxn 2600
#define mxe 26000
#define inf 0x3f3f3f3f
struct SAP{
int dis[mxn],pre[mxn],gap[mxn],arc[mxn],f[mxe],cap[mxe];
int head[mxn],nxt[mxe],vv[mxe],e;
void init(){e=0;memset(head,-1,sizeof(head));}
void addedge(int u,int v,int c){
vv[e]=v,cap[e]=c,nxt[e]=head[u],head[u]=e++;
vv[e]=u,cap[e]=0,nxt[e]=head[v],head[v]=e++;
}
int max_flow(int s,int t,int n){
int q[mxn],j,mindis,ans=0,ht=0,tl=1;
int u,v,low;
bool found,vis[mxn];
memset(dis,0,sizeof(dis));
memset(gap,0,sizeof(gap));
memset(vis,0,sizeof(vis));
memset(arc,0,sizeof(arc));
memset(f,0,sizeof(f));
q[0]=t,vis[t]=true,dis[t]=0,gap[0]=1;
while(ht<tl){
int u = q[ht++];
for(int i=head[u];i!=-1;i=nxt[i]){
v = vv[i];
if(!vis[v]){
vis[v]=true;
dis[v]=dis[u]+1;
q[tl++]=v;
gap[dis[v]]++;
arc[v]=head[v];
}
}
}
u=s;low=inf;pre[s]=s;
while(dis[s]<n){
found = false;
for(int &i = arc[u];i!=-1;i=nxt[i]){
if(dis[vv[i]]==dis[u]-1 && cap[i]>f[i]){
found = true; v=vv[i];
low = min(low, cap[i]-f[i]);
pre[v]=u;u=v;
if(u==t){
while(u!=s){
u=pre[u];
f[arc[u]]+=low;
f[arc[u]^1]-=low;
}
ans+=low;low=inf;
}
break;
}
}
if(found) continue;
mindis = n;
for(int i=head[u];i!=-1;i=nxt[i]){
if(mindis>dis[vv[i]] && cap[i]>f[i]){
mindis = dis[vv[j=i]];
arc[u]=i;
}
}
if(--gap[dis[u]]==0) return ans;
dis[u] = mindis+1;
gap[dis[u]]++;
u=pre[u];
}
return ans;
}
}sap;
char maze[55][55];
int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
int main(){
int t,n,m,ca=0;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) scanf("%s",maze[i]+1);
for(int i=0;i<=n+1;++i) maze[i][0]=maze[i][m+1]=‘D‘;
for(int j=0;j<=m+1;++j) maze[0][j]=maze[n+1][j]=‘D‘;
sap.init();
int src = (n+2)*(m+2);
int des = src+1;
for(int i=0;i<=n+1;++i){
for(int j=0;j<=m+1;++j){
int u = i*(m+2)+j;
if((i^j)&1){
if(maze[i][j]==‘D‘) sap.addedge(u,des,inf);
if(maze[i][j]==‘.‘) sap.addedge(src,u,inf);
}else {
if(maze[i][j]==‘.‘) sap.addedge(u,des,inf);
if(maze[i][j]==‘D‘) sap.addedge(src,u,inf);
}
for(int k=0;k<4;++k){
int ii=i+dx[k];
int jj=j+dy[k];
if(ii<0 || jj<0 || ii>n+1||jj>m+1) continue;
int u = i*(m+2)+j;
int v = ii*(m+2)+jj;
sap.addedge(u,v,1);
}
}
}
int mf = sap.max_flow(src,des,des+1);
int sum = (n+1)*(m+2)+(n+2)*(m+1);
printf("Case %d: %d\n",++ca,sum-mf);
}
return 0;
}
原文:http://www.cnblogs.com/nextbin/p/4072171.html