注:模板以hdu 2544 为例
2 1 1 2 3 3 3 1 2 5 2 3 5 3 1 2 0 0
3 2
一.Bellman-Ford算法
介绍:
贝尔曼-福特算法(Bellman-Ford)是由理查德·贝尔曼(Richard Bellman) 和 莱斯特·福特 创立的,求解单源最短路径问题的一种算法。有时候这种算法也被称为
Moore-Bellman-Ford 算法,因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行V-1次松弛操作,得到所有可能的最短路径。其优于迪科斯彻算法的
方面是边的权值可以为负数、实现简单,缺点是时间复杂度过高,高达O(VE)。但算法可以进行若干种优化,提高了效率。
算法:
贝尔曼-福特算法与迪科斯彻算法类似,都以松弛操作为基础,即估计的最短路径值渐渐地被更加准确的值替代,直至得到最优解。在两个算法中,计算时每个边之间的
估计距离值都比真实值大,并且被新找到路径的最小长度替代。 然而,迪科斯彻算法以贪心法选取未被处理的具有最小权值的节点,然后对其的出边进行松弛操作;而贝尔曼-
福特算法简单地对所有边进行松弛操作,共|V | ? 1次,其中 |V |是图的点的数量。在重复地计算中,已计算得到正确的距离的边的数量不断增加,直到所有边都计算得到了正确
的路径。这样的策略使得贝尔曼-福特算法比迪科斯彻算法适用于更多种类的输入。
贝尔曼-福特算法的最多运行O(|V|·|E|)次,|V|和|E|分别是节点和边的数量)。(来源于维基百科)
个人注:
Bellman_Ford算法,求单源到其它节点的最短路,可以处理含有负权的边,并且能判断图中是否存在负权回路(这一条在一些题中也有应用) ,无向图转化为有向图,边数加倍,构造边结构体,没用到邻接矩阵 。
模板:
const int maxNodeNum=110;//最多节点个数
const int maxEdgeNum=10010;//最多边条数
int nodeNum,edgeNum;//节点,有向边个数
int dis[maxNodeNum];//从单源点到各个点的距离
const int inf=0x3f3f3f3f;//边的权重无穷大数
bool loop;//判断是否存在负权回路
struct Edge
{
int s,e,w;
}edge[maxEdgeNum*2];//构造边,这里因为是无向图,要看成有向处理。
void bellman_ford(int start)
{
//第一步:赋初值
for(int i=1;i<=nodeNum;i++)
dis[i]=inf;
dis[start]=0;
//第二步,对边进行松弛更新操作
for(int i=1;i<=nodeNum-1;i++)//最短路径为简单路径不可能含有环,图中最多有nodeNum-1条边
{
bool ok=0;
for(int j=1;j<=edgeNum;j++)
{
if(dis[edge[j].s]+edge[j].w<dis[edge[j].e])//松弛
{
dis[edge[j].e]=dis[edge[j].s]+edge[j].w;
ok=1;
}
}
if(ok==0)
break;
}
//第三步,判断图中是否存在负权环
loop=0;
for(int i=1;i<=edgeNum;i++)
if(dis[edge[i].s]+edge[i].w<dis[edge[i].e])
loop=1;
}
int main()//125MS
{
while(cin>>nodeNum>>edgeNum&&(nodeNum||edgeNum))
{
int from,to,w;
int cnt=1;
for(int i=1;i<=edgeNum;i++)//无向图,一条无向边看为两条有向边
{
cin>>from>>to>>w;
edge[cnt].s=edge[cnt+1].e=from;
edge[cnt].e=edge[cnt+1].s=to;
edge[cnt++].w=w;
edge[cnt++].w=w;//切记,不能写成 edge[cnt++]=edge[cnt++].w;
}
edgeNum*=2;//无向图
bellman_ford(1);
cout<<dis[nodeNum]<<endl;
}
return 0;
}
介绍:
求单源最短路的SPFA算法的全称是:Shortest Path Faster Algorithm。 SPFA算法是西南交通大学段凡丁于1994年发表的。松弛操作必定只会发生在最短路径前导节点
松弛成功过的节点上,用一个队列记录松弛过的节点,可以避免了冗余计算。复杂度可以降低到O(kE),k是个比较小的系数(并且在绝大多数的图中,k<=2,然而在一些精心构
造的图中可能会上升到很高).
个人注:
SPFA算法,是对bellman_ford算法的优化,采用队列,在队列中取点对其相邻的点进行松弛操作 。如果松弛成功且相邻的点不在队列中,就把相邻的点加入队列,被取的
点出队,并把它的状态(是否在队列中) 改为否,vis[i]=0,同一个节点可以多次进入队列进行松弛操作 。
这样的题操作步骤:首先建立邻接矩阵,邻接矩阵初始化为inf,注意需要判断一下输入的边是否小于已有的边,取最小的那个,因为可能有重边, 建立完邻接矩阵,写SPFA
函数,dis[]数组初始化为inf,源点dis[start]=0 。
模板:
const int maxNodeNum=110;//最多节点个数
const int maxEdgeNum=10010;//最多边条数
const int inf=0x3f3f3f3f;//边的权重无穷大数
int nodeNum,edgeNum;//节点,有向边个数
int dis[maxNodeNum];//从单源点到各个点的距离
bool vis[maxNodeNum];//某个节点是否已经在队列中
int mp[maxNodeNum][maxNodeNum];//建立邻接矩阵
void SPFA(int start)
{
//第一步:建立队列,初始化vis,dis数组,并把源点加入队列中,修改其vis[]状态
queue<int>q;
memset(vis,0,sizeof(vis));
for(int i=1;i<=nodeNum;i++)
dis[i]=inf;
dis[start]=0;
q.push(start);
vis[start]=1;
//第二步:在队列中取点,把其vis状态设为0,对该点相邻的点(连接二者的边)进行松弛操作,修改相邻点的dis[]
//并判断相邻的点vis[]状态是否为0(不存在于队列中),如果是,将其加入到队列中
while(!q.empty())
{
int from=q.front();
q.pop();
vis[from]=0;//别忘了这一句,哎
for(int i=1;i<=nodeNum;i++)
{
if(dis[from]+mp[from][i]<dis[i])
{
dis[i]=dis[from]+mp[from][i];
if(!vis[i])//要写在松弛成功的里面
{
q.push(i);
vis[i]=1;
}
}
}
}
}
int main()//109MS
{
while(cin>>nodeNum>>edgeNum&&(nodeNum||edgeNum))
{
int from,to,w;
memset(mp,inf,sizeof(mp));//初始化
for(int i=1;i<=edgeNum;i++)//无向图,一条无向边看为两条有向边
{
cin>>from>>to>>w;
if(w<mp[from][to])
mp[from][to]=mp[to][from]=w;
}
SPFA(1);
cout<<dis[nodeNum]<<endl;
}
return 0;
}
介绍:
Floyd-Warshall算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传
递闭包。
Floyd-Warshall算法的时间复杂度为O(N^3),空间复杂度为O(N^2)。
算法:
Floyd-Warshall算法的原理是动态规划。
设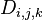 为从
为从 到
到 的只以
的只以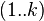 集合中的节点为中间节点的最短路径的长度。
集合中的节点为中间节点的最短路径的长度。
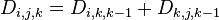 ;
;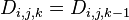 。
。
因此,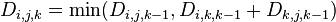 。
。
在实际算法中,为了节约空间,可以直接在原来空间上进行迭代,这样空间可降至二维。(见下面的算法描述)
for k ← 1 to n do
for i ← 1 to n do
for j ← 1 to n do
if ( ) then
) then
 ←
← 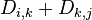 ;
;
个人注:
解释一下 设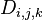 为从
为从 到
到 的只以
的只以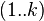 集合中的节点为中间节点的最短路径的长度
这一句话,也就是说从i到j这条路径上经过的点(不包括两头的i,j)只能在(1,2...k)中,经过点的长度不超过k。下面以具体例子来阐述该算法(参考数据结构课本)。如图:
集合中的节点为中间节点的最短路径的长度
这一句话,也就是说从i到j这条路径上经过的点(不包括两头的i,j)只能在(1,2...k)中,经过点的长度不超过k。下面以具体例子来阐述该算法(参考数据结构课本)。如图:
建议把这个图单独保存,看流程的时候只看邻接矩阵容易晕,还是看图比较直接。
该图的邻接矩阵为:
考虑顶点几,也就是拿第几个顶点当作中间点。
考虑顶点0,A0[i][j]表示由顶点i到顶点j经由点0的最短路径长度,经过比较,没有任何路径得到修改。比较的过程是:
A[0][0]与A[0][0]+A[0][0]比较, A[0][1]与A[0][0]+A[0][1]比较,
A[0][2]与A[0][0]+A[0][2]比较, A[0][3]与A[0][0]+A[0][3]比较,
A[1][0]与A[1][0]+A[0][0]比较, A[1][1]与A[1][0]+A[0][1]比较,
A[1][2]与A[1][0]+A[0][2]比较,
A[1][3]与A[1][0]+A[0][3]比较,
.......
....
A[3][0]与A[3][0]+A[0][0]比较, A[3][1]与A[3][0]+A[0][1]比较,
A[3][2]与A[3][0]+A[0][2]比较,
A[3][3]与A[3][0]+A[0][3]比较,
可以看出中间点始终是0,因为我们当前考虑的就是顶点0
比较完得到的邻接矩阵没有变化。
考虑顶点1.顶点0到顶点2由原来的没有路径(无穷大)变为0-1-2,因为A[0][1]+A[1][2]=9<无穷大,修改A[0][2]为9,其他值经过比较无变化。
考虑顶点2:
顶点1到顶点0由原来没有路径变为0-1-2,长度为7,A[1][0]修改为7;顶点3到顶点0由原来没有路径变为3-2-0,长度为4,A[3][0]修改为4
顶点3到顶点1由原来没有路径变为3-2-1,长度为4,A[3][1]修改为4,其他数值不用修改。
考虑顶点3:
顶点0到顶点2原来的最短路径为9,0-1-2,现有一条更短的路径0-3-2,A[0][2]>A[0][3]+A[3][2]=8,A[0][2]修改为8;
顶点1到顶点0原来的最短路径为7,1-2-0,现有一条更短的路径1-3-2-0,A[1][0]>A[1][3]+A[3][0]=6,A[1][0]修改为6;
顶点1到顶点2原来的最短路径为4,1-2, 现有一条更短的路径1-3-2,A[1][2]>A[1][3]+A[3][2]=3,A[1][2]修改为3,其他数值不改变。
最后得到的各顶点最短路径邻接矩阵为:
四:Dijstra算法
算法:
这个算法是通过为每个顶点 v 保留目前为止所找到的从s到v的最短路径来工作的。初始时,原点 s 的路径长度值被赋为 0 (d[s] = 0),若存在能直接到达的边(s,m),则把d[m]设为w(s,m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大,即表示我们不知道任何通向这些顶点的路径(对于
V 中所有顶点 v 除 s 和上述 m 外 d[v] = ∞)。当算法退出时,d[v] 中存储的便是从 s 到 v 的最短路径,或者如果路径不存在的话是无穷大。 Dijkstra 算法的基础操作是边的拓展:如果存在一条从 u 到 v 的边,那么从 s 到 v 的最短路径可以通过将边(u, v)添加到尾部来拓展一条从 s 到 v 的路径。这条路径的长度是 d[u] + w(u, v)。如果这个值比目前已知的 d[v] 的值要小,我们可以用新值来替代当前 d[v] 中的值。拓展边的操作一直运行到所有的 d[v]
都代表从 s 到 v 最短路径的花费。这个算法经过组织因而当 d[u] 达到它最终的值的时候每条边(u, v)都只被拓展一次。
算法维护两个顶点集 S 和 Q。集合 S 保留了我们已知的所有 d[v] 的值已经是最短路径的值顶点,而集合 Q 则保留其他所有顶点。集合S初始状态为空,而后每一步都有一个顶点从 Q 移动到 S。这个被选择的顶点是 Q 中拥有最小的 d[u] 值的顶点。当一个顶点 u 从 Q 中转移到了 S 中,算法对每条外接边 (u, v) 进行拓展。
个人注:
dijkstra算法求最短路,单源最短路,不能处理带有负权的图,思想为单源点加入集合,更新dis[]数组,每次取dis[]最小的那个点,贪心思想,加入集合,再次更新dis[]数组,取点加入集合,直到所有的点都加入集合中.
模板:
const int maxNodeNum=110;//最多节点个数
const int maxEdgeNum=10010;//最多边条数
const int inf=0x3f3f3f3f;
int nodeNum,edgeNum;//节点,有向边个数
int mp[maxNodeNum][maxNodeNum];//建立邻接矩阵
int dis[maxNodeNum];//dis[i]为源点到i的最短路径
bool vis[maxNodeNum];//判断某个节点是否已加入集合
void dijkstra(int start)
{
//**第一步:初始化,dis[]为最大,vis均为0(都未加入集合)
memset(dis,inf,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[start]=0; //<span style="color:#ff0000;">注意不能写vis[start]=1,因为这时候第一个节点还没有被访问,下面循环中,第一个选择的就是第一个节点,切记</span>
//**第二步:找dis[]值最小的点,加入集合,并更新与其相连的点的dis[]值
//一开始集合里没有任何点,下面的循环中,第一个找到的点肯定是源点
for(int i=1;i<=nodeNum;i++)
{
//寻找dis[]最小的点,加入集合中
int MinNumber,Min=inf;//MinNumber为dis[]值最小的点的编号
for(int j=1;j<=nodeNum;j++)
{
if(dis[j]<Min&&!vis[j])
{
Min=dis[j];
MinNumber=j;
}
}
//找到dis[]最小的点,加入集合,更新与其相连的点的dis值
vis[MinNumber]=1;
for(int j=1;j<=nodeNum;j++)
if(dis[MinNumber]+mp[MinNumber][j]<dis[j])
dis[j]=dis[MinNumber]+mp[MinNumber][j];
}
}
int main()//109MS
{
while(cin>>nodeNum>>edgeNum&&(nodeNum||edgeNum))
{
int from,to,w;
memset(mp,inf,sizeof(mp));//初始化
for(int i=1;i<=edgeNum;i++)//无向图,一条无向边看为两条有向边
{
cin>>from>>to>>w;
if(w<mp[from][to])
mp[from][to]=mp[to][from]=w;
}
dijkstra(1);
cout<<dis[nodeNum]<<endl;
}
return 0;
}
[图论] 最短路径(Bellman-Ford , SPFA , Floyed , Dijkstra)
原文:http://blog.csdn.net/sr_19930829/article/details/40897183