贝塞尔曲线,可以通过三个点,来确定一条平滑的曲线,是图形开发中的重要工具,实际的是一个图形做圆周运动,不过不是简单的关键帧动画那样,是计算出了很多点,当然还是用的关键帧动画,即使用CAKeyframeAnimation
Bezier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线, 曲线定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。1962年, 法国数学家Pierre Bezier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照哦啊这样的公式绘制出来的曲线就是用他的姓氏来命名,称为贝塞尔曲线
一下公式中:B(t)为时间下点的坐标
P0为起点,Pn为终点,Pi为控制点
一阶贝塞尔曲线(线段):
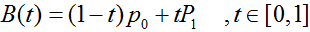
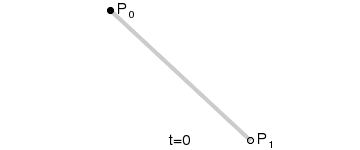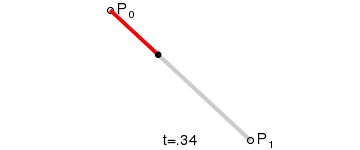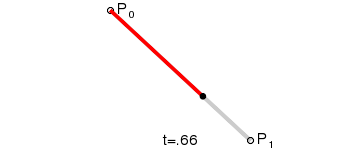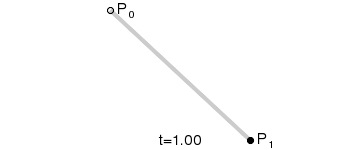
意义:由P0至P1的连续点,描述一条线段
二阶贝塞尔曲线(抛物线):

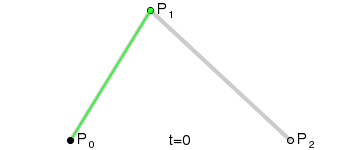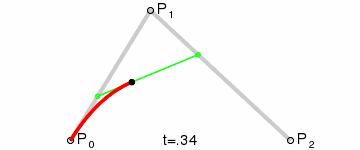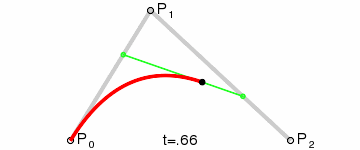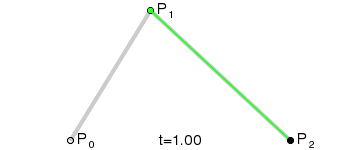
原理:
由P0至P1的连续点Q0,描述一条线段
由P1至P2的连续点Q1,描述一条线段
由Q0至Q1的连续点B(t), 描述一条二次贝塞尔曲线
经验:P1-P0为曲线在P0处的切线
三阶贝塞尔曲线:


通用公式:
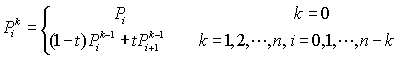
原文:http://my.oschina.net/syc2013/blog/343567