使用matlab用优化后的梯度下降法求解达最小值时参数

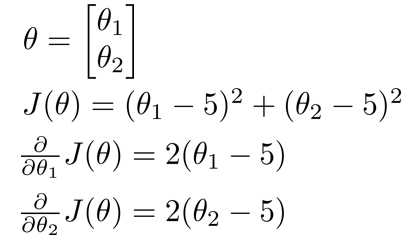
function [jVal, gradient]
           = costFunction(theta)

jVal = (theta(1)-5)^2 + ...           (theta(2)-5)^2;

gradient = zeros(2,1);

gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);

options = optimset(‘GradObj’, ‘on’, ‘MaxIter’, ‘100’);

[optTheta, functionVal, exitFlag] ...

     = fminunc(@costFunction, initialTheta, options);