·背景
最近乘闲暇之余初探了HMM(隐马尔科夫模型),觉得还有点意思,但是网上的教程都超级枯草,可读性很差,抄来抄去的,一堆公式仍在你面前,谁能搞的懂(但园内的两篇写的还算不错。真才实学)。在熬制3天后,把这篇心得反馈给各位码友,为了更加生动的说明模型,特举例三国杀的"于吉"以便加深各位印象。

·于吉
武将技:【蛊惑】——你可以说出任何一种基本牌或非延时类锦囊牌,并正面朝下使用或打出一张手牌。若无人质疑,则该牌按你所述之牌结算。若有人质疑则亮出验明:若为真,质疑者各失去1点体力;若为假,质疑者各摸1张牌。无论真假,弃置被质疑的牌。仅当被质疑的牌为红桃花色且为真时,该牌仍然可以进行结算。最大的意义在于猜测真假,也就是HMM中的隐藏队列。



·HMM 五对象
·观察队列:也就是对手打出的声明牌序,例如【杀、杀、桃、杀、南蛮】。这3张牌个人感觉算是于吉回合内声明频率最高的3张牌。
·隐藏队列:也就是对手打出该张牌时是真?是假?,例如【真、真、假、假、真】,这个是HMM之后要计算的对象之一。
·初始状态Matrix P/Pie:声明第一张牌时,是真是假的概率。
·状态转移Matrix A:从声明第二章牌开始,由真变假,或假变真,或真变真,或假变假的概率。
·混淆矩阵Matrix B:每次声明时的真假心态下,该将什么牌声明成什么牌。
·HMM 两大问题(还有一个学习就不写了)
·评估问题:该轮的声明牌序,其中存在假牌的可能性有多高?
·解码问题:该轮的声明牌序,其中哪几张牌可能为假牌?
·HMM 评估算法过程
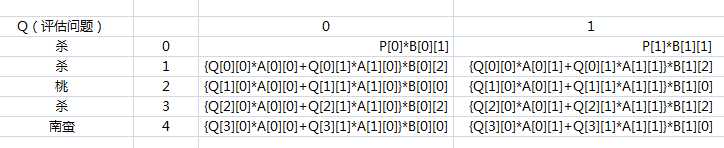
·HMM 解码算法过程

·HMM测算结果
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 |
Complie Doneact:0 Q[0][0]:0.16 Q[0][1]:0.1 act:0 Q[1][0]:0.0332 Q[1][1]:0.047 act:1 Q[2][0]:0.021128 Q[2][1]:0.005476 act:0 Q[3][0]:0.003302 Q[3][1]:0.005047 act:2 Q[4][0]:0.00220564 Q[4][1]:0.00085047 Last Sum Prob=0.00305611act:0 Q[0][0]:0.16 Q[0][1]:0.1 act:0 com[0]0.096 comp[1]0.07 Q[1][0]:0.0192 com[0]0.064 comp[1]0.03 Q[1][1]:0.032 act:1 com[0]0.01152 comp[1]0.0224 Q[2][0]:0.00896 com[0]0.00768 comp[1]0.0096 Q[2][1]:0.00192 act:0 com[0]0.005376 comp[1]0.001344 Q[3][0]:0.0010752 com[0]0.003584 comp[1]0.000576 Q[3][1]:0.001792 act:2 com[0]0.00064512 comp[1]0.0012544 Q[4][0]:0.00050176 com[0]0.00043008 comp[1]0.0005376 Q[4][1]:0.00016128 Last Max Prob:0.00050176Path[0][0]=-1 Path[0][1]=-1Path[1][0]=0 Path[1][1]=0Path[2][0]=1 Path[2][1]=1Path[3][0]=0 Path[3][1]=0Path[4][0]=1 Path[4][1]=1real 0m0.001suser 0m0.000ssys 0m0.000s |
Last Sum Prob=0.00305611,个人理解更贴近于本次序列不作弊的可能性。
Path[i][j]来源t-1时刻两种隐藏状态的概率对比,前面<后面 为1,前面>后面 为0。从1和0的区别看,0的出现意味着该张牌声明时作假可能性更高。
·不足之处
·源码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141 |
#include <iostream>#include <vector>#include <map>#include <iomanip>#include <algorithm>using namespace std;vector<string> v_ob;vector<string> v_hide_real;map<string,int> m_ob;map<string,int> m_p;double P[2]={0.8,0.2}; //初始状态矩阵double A[2][2]={{0.6,0.4},{0.7,0.3}}; //状态转移矩阵double B[2][3]={{0.2,0.4,0.4},{0.5,0.2,0.3}}; //混淆矩阵void Para_init(); //初始化观察队列void Forward(); //算前向void Viterbi();int main(){ Para_init(); Forward(); Viterbi();}//vector 作为函数入参数 void show_vector(vector <int> &vecTest)void Viterbi(){ int LEN=v_ob.size(); int M=2; double Q[LEN][M]; double Path[LEN][M]; for(int i=0;i<LEN;i++) { int act=m_ob[v_ob[i]]; //当天活动 cout<<"act:"<<act<<"\t"; for(int j=0;j<M;j++) { if(i==0) { Q[i][j]=P[j]*B[j][act]; Path[i][j]=-1; } else { double compare[2]; for(int z=0;z<M;z++) { compare[z]=Q[i-1][z]*A[z][j]; } if(compare[0]<compare[1]) { Path[i][j]=1;} else { Path[i][j]=0;} Q[i][j]=max(compare[0],compare[1])*B[j][act]; cout<<"com[0]"<<left<<setw(11)<<compare[0]<<" "<<"comp[1]"<<setw(11)<<compare[1]<<"\t"; } cout<<"Q["<<i<<"]["<<j<<"]:"<<left<<setw(11)<<Q[i][j]<<"\t"; } cout<<endl; } cout<<endl; cout<<"Last Max Prob:"<<max(Q[LEN-1][0],Q[LEN-1][0])<<endl; cout<<endl; for(int i=0;i<LEN;i++) { for(int j=0;j<M;j++) {cout<<"Path["<<i<<"]["<<j<<"]="<<Path[i][j]<<"\t";} cout<<endl; }}void Forward(){ int LEN=v_ob.size(); int M=2; double Q[LEN][M]; for(int i=0;i<LEN;i++) { int act=m_ob[v_ob[i]]; //当天活动 cout<<"act:"<<act<<"\t"; for(int j=0;j<M;j++) { //首行判断 if(i==0) { Q[i][j]=P[j]*B[j][act]; //cout<<"j="<<j<<"act="<<act<<endl; } else { double sum=0; for(int z=0;z<M;z++) { // cout<<"tmp="<<Q[i-1][z]*A[z][j]<<" "; sum+=Q[i-1][z]*A[z][j]; } Q[i][j]=sum*B[j][act]; } cout<<"Q["<<i<<"]["<<j<<"]:"<<left<<setw(11)<<Q[i][j]<<"\t"; } cout<<endl; } double sum=0; for(int j=0;j<M;j++) { sum+=Q[LEN-1][j]; } cout<<endl; cout<<"Last Sum Prob="<<sum<<endl; cout<<endl;}void Para_init(){//add oberser_list v_ob.push_back("kill"); v_ob.push_back("kill"); v_ob.push_back("tao"); v_ob.push_back("kill"); v_ob.push_back("man");// dict m_ob.insert(make_pair("kill",0)); m_ob.insert(make_pair("tao",1)); m_ob.insert(make_pair("man",2)); m_p.insert(make_pair("true",0)); m_p.insert(make_pair("false",1));} |
本人才疏学浅,各位麻友轻拍砖~~~ ^_^
用HMM(隐马)图解三国杀的于吉“质疑”,布布扣,bubuko.com
原文:http://www.cnblogs.com/zacard-orc/p/3569881.html