第一讲中我们学习了一个机器学习系统的完整框架,包含以下3部分:训练集、假设集、学习算法
一个机器学习系统的工作原理是:学习算法根据训练集,从假设集合H中选择一个最好的假设g,使得g与目标函数f尽可能低接近。H称为假设空间,是由一个学习模型的参数决定的假设构成的一个空间。而我们这周就要学习一个特定的H——感知器模型。
感知器模型在神经网络发展历史中占有特殊地位,并且是第一个具有完整算法描述的神经网络学习算法(称为感知器学习算法:PLA)。这个算法是由一位心理学家Rosenblatt在1958年提出来的,因此它也叫做Rosenblatt感知器。感知器是用于线性可分模式分类的最简单的神经网络模型,它由一个具有可调突触权值和偏置的神经元组成。用于调节神经网络中参数的算法最早出现在Rosenblatt(1958,1962)提出的用于其脑感知模型的一个学习过程中(即PLA)。Rosenblatt证明了当输入数据的模式是线性可分的时候,感知器学习算法能够在有限步迭代后收敛,并且决策面是位于两类之间的超平面。算法的收敛性证明被称为感知器收敛定理。那么首先介绍一下什么是感知器。
下图是一个感知器的示意图:
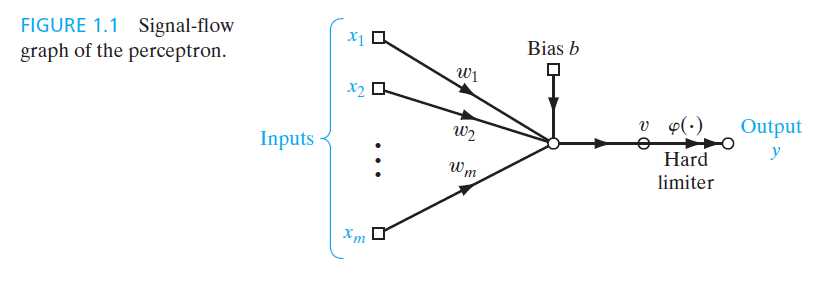
(图摘自Neural Networks and Learning Machines,3rd Edition)
一个感知器由三个部分组成:
1)突触权值(即图中的$w_1,w_2,...,w_m$)
2)求和单元,用突触权值对输入进行加权并加上偏置,得到诱导局部域(v)
3)激活函数(即图中的hard limiter)用于限制诱导局部域输出的振幅,在感知器中,使用符号函数来限制输出(当v>0时输出为1,反之为-1)
以上神经元称为McCulloch-Pitts模型,可以用两条数学公式概括:
\[ v = \sum_{i=1}^m w_i x_i + b \]
\[ y = \phi(v) = \begin{cases} 1 & if \quad v >0\\ -1 & otherwise\end{cases} \]
关于偏置的作用,直观上可以这样理解,当$\sum_{i=1}^m w_i x_i >-b$时输出为1,当$\sum_{i=1}^m w_i x_i \leq -b$时输出为-1,这里$-b$实际上是一个阈值,而求和单元求和的结果可以认为是一个根据输入特征进行打分的函数,突触权值是特征的重要性或者可以理解为每个特征的分数,当分数超过阈值时,我们给它分到+1代表的类,不超过则分到-1.是不是有点像老师改卷的过程?权值是每道题的分数,输入是学生每道题的对错情况,输出是这个学生最后的总分,当这个总分超过一个阈值(比如60分)时,给他pass,否则不给他pass。
我们可以把偏置$b$看作一个特殊的突触单元,$x_0=+1$,$w_0=b$,分别加入到输入向量和权值向量中。这样,感知器的输出可以表示为一个更为简洁的形式$f(x)=\sum_{i=0}^m w_ix_i$,又可以简化为一个向量形式,即$f(x)=w^Tx$,其中$w=(w_0,w_1,...,w_m)^T$,$x=(x_0,x_1,...,x_m)^T$它们都是m+1维的向量。不过为了方便后面的推导,还是把它拆开来写:$f(x)=w^Tx+b$
感知器模型实际上定义了一组超平面$w^Tx+b=0$,称为分离超平面。感知器模型实际上是关于$w,b$的函数,这个超平面将空间分为两半,一半是由满足$w^Tx+b> 0$的点(标记为+1)组成,另一半由$w^Tx+b\leq 0$定义(标记为-1)。给定一个点$x_i$,我们可以用以下的决策函数预测它的标号:
$$ f(x) = sign(w^Tx+b) $$
其中sign是符号函数,当括号里的项大于时,输出为+1;小(等)于0时,输出为-1.给定一个训练数据集$\mathcal{D}=\{(x_1,y_1),...,(x_n,y_n)\}$的情形下,我们的目标是尽可能地满足$f(x_i)=y_i$,但一开始由于我们事先不知道超平面长什么样,难免会分错,而PLA算法告诉我们的是,我们可以利用这些错分的点来修正权值向量$w,b$,使之往正确的位置靠近。为此,我们首先需要定义一个函数,来衡量一次预测错误的程度,这个函数称为损失函数。一个合理的选择是误分类点的总数,但是这个函数不是$w,b$的可导函数,因此我们用了另一个函数作为替代,即误分类点到超平面的总距离,这个准则的好处是关于$w,b$可导,因此可以使用梯度下降算法来优化。下面我来解释一下为什么用误分类点到超平面的距离来作为损失函数。
下图是一个二维的超平面
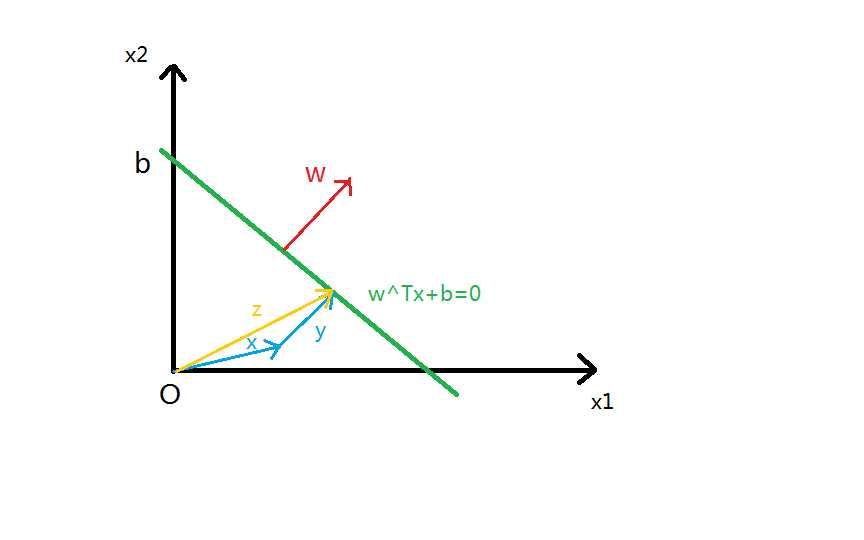
上图中,点x到超平面的距离是
$$ \frac{1}{\left\|w\right\|}|w^Tx+b| $$
推导过程:
由图中的关系有:$x+y=z$,由于$y$与法向量$w$共线,可设$y=\lambda w$,则$z=x+\lambda w$
因为$z$在超平面上,故$w^Tz+b=0$,得到$w^Tx+\lambda w^Tw + b = 0$
于是有$\lambda = \frac{-(w^Tx+b)}{w^Tw}$
距离为$d=|y|=|\lambda|\left\|w\right\|=\frac{1}{\left\|w\right\|}|w^Tx+b|$
直观上来理解,误分类点离超平面越远,我们就需要花越多的代价将$w,b$纠正,因此损失函数较大。而我们的目标就是使这种损失在平均意义上最小,即
$$ L(w,b)=\sum_{x_i\in M} -y_i(w^Tx_i+b) $$
其中$M$是误分类点的集合,$-y_i(w^Tx_i+b)$实际上是$|w^Tx_i+b|(x_i\in M)$,因为对于误分类的点来说,$y_i$和$w^Tx_i+b$的符号一定是相反的,所以$-y_i(w^Tx_i+b)$一定是正数,实际上,$y_i(w^Tx_i+b)$有一个专门的名字,称为函数间隔,这个概念在SVM中也有出现。这里我们的目标是最小化L,方法是用L的梯度来修正w和b。
我们求$L$关于$w,b$的梯度:
$ \frac{\partial L}{\partial w}=-\sum_{x_i\in M}y_ix_i $
$ \frac{\partial L}{\partial b} =-\sum_{x_i\in M}y_i$
这里,因为一次更新采用所有样本太费时,我们一次从分错的样本中随机挑选出一个来更新,此方法称为随机梯度下降算法。对应w,b的更新式为
$$ w \leftarrow w + \eta y_ix_i $$
$$ b \leftarrow b + \eta y_i $$
式中$\eta$为学习率,在实现时,可以先随机生成一个排列,再遍历这个序列直到遇到第一个分错的样本,。
为了方便后面的推导,把$b$加入$w$,令$w=(w,-b)$,$x=(x,1)$,则$f(x)=w^Tx$,通常把$w$称为权重向量。对应的更新式为
$$w \leftarrow w + \eta y_ix_i$$
这个更新式就是感知器学习算法PLA的核心。
下面是PLA算法的完整描述:
输入:训练集T,学习率$\eta$
输出:w,b;感知器模型$f(x)=sign(w^Tx+b)$
过程:
(1)初始化$w_0$,可以全部初始化为0
(2)选取数据$(x_i,y_i)$
(3)如果$y_i(w^Tx_i+b)\leq 0$
$$w \leftarrow w + \eta y_ix_i$$
(4)跳至(2),直至训练集中没有误分类点
注意到,误分类点有这样一个性质:$y_i(w^Tx_i+b)\leq 0$。最后得到的超平面一定是能够将所有正/负样本分离开来的,我们把这种性质叫做线性可分性。
设最终收敛的权重向量是$w_f$,这一性质可以表示为:对于所有的样本点,都有
$$ y_iw_f^Tx_i \geq 0 $$
这个算法看起来很简洁,有人会问,这么简单的算法真的起作用吗,能收敛吗? 答案是肯定的。也就是说,可以证明算法一定能收敛,并且可以求出收敛次数的上限。
假设第t次迭代时w的值为$w(t)$,可以证明下一轮迭代得到的权重向量$w(t+1)$一定比上一轮与$w_f$的夹角余弦更小,记$\cos\theta(t+1)=\frac{w(t+1)^Tw_f}{\left\|w(t+1)\right\|\left\|w_f\right\|}$,则$\cos\theta(t+1) < \cos\theta(t)$。这意味着经过每一轮迭代后$w(t)$都比之前更靠近$w_f$。
后来想想这点不一定成立,还需要实验来验证,但可以证明的是,随着迭代次数的增加,$w(t)$越来越接近$w_f$,最后收敛于$w_f$
下面来证明这个结论。在证明过程中,引入几个记号。
(1)$R=\max_{1\leq i\leq N}\left\|x_i\right\|$
(2)$\gamma=\min\{y_iw_f^Tx_i\}$
证明过程:
首先考察$\cos\theta(t)=\frac{w(t)^Tw_f}{\left\|w(t)\right\|\left\|w_f\right\|}$的分子:
$$w(t)^Tw_f = (w(t-1)+\eta y_i(t-1)x_i(t-1))^Tw_f = w(t-1)^Tw_f + \eta y_i(t-1) w_f^Tx_i(t-1) \geq w(t-1)^Tw_f + \eta \gamma\geq w(t-2)^Tw_f+2\eta\gamma\geq\cdots\geq t\eta\gamma$$
另一方面,
$$\left\|w(t)\right\|^2=\left\|w(t-1)\right\|^2+\eta^2y_i(t-1)^2\left\|x_i(t-1)\right\|^2+2\eta y_i(t-1)w(t-1)^Tx_i(t-1)\leq \left\|w(t-1)\right\|^2+\eta^2R^2\leq\cdots\leq t\eta^2R^2$$
$$ \left\|w(t+1)\right\|\leq \sqrt{t+1}\eta R$$
因此,$$\cos\theta(t) \geq \frac{t\gamma}{\left\|w_f\right\|\sqrt{t}R}=\sqrt{t}(\frac{\gamma}{\left\|w_f\right\|R})$$
由此我们可以知道$\cos\theta(t)$的下限是关于$\sqrt{t}$单调递增的函数,而$\cos\theta(t)$最多不超过1,因此随着迭代次数的增加,这个下限会越来越趋近于1,直至收敛。这就证明了经过有限次迭代后,$w(t)$会收敛于$w_f$
原文:http://www.cnblogs.com/wacc/p/3848418.html