NG的课件1也讲到了牛顿法,它对应的update rule是
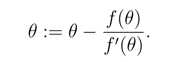
? ?
? ?
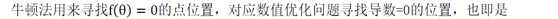
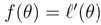
? ?
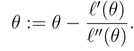
? ?
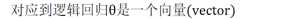
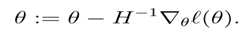
? ?
H对应Hessian矩阵
http://en.wikipedia.org/wiki/Hessian_matrix

? ?
http://aria42.com/blog/2014/12/understanding-lbfgs/
给出了关于牛顿法更详细的解释:
? ?
将函数做泰勒展开 http://en.wikipedia.org/wiki/Taylor_series
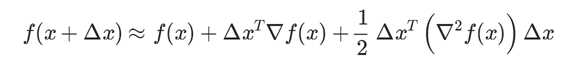
对比单变量函数泰勒展开公式:
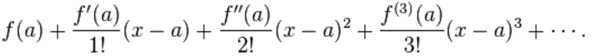
? ?
? ?
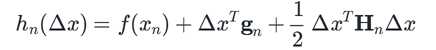
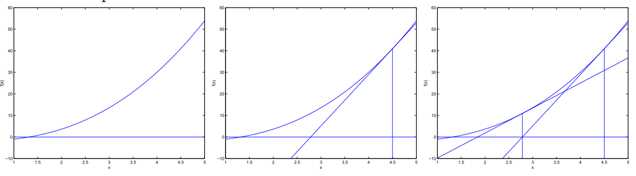
考虑我们需要找一阶导数是0的位置
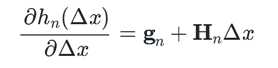
? ?
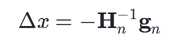
和ng课件给出的一致。
? ?
牛顿法和梯度下降相比收敛更加快速,但是每次迭代的计算量更大(n+1,n+1)维度的hessian矩阵的计算,但是如果n不是特别大那么整体来看牛顿法更快。
? ?
原文:http://www.cnblogs.com/rocketfan/p/4152391.html