题意: 给出两点的经纬度,求两点的球面距离与直线距离之差。
解法: 我们先算出球面距离,然后可以根据球面距离算出直线距离。
球面距离公式: R*acos(sin(W1)*sin(W2)+cos(W1)*cos(W2)*cos(J1-J2)); ( W1,W2 为两点的纬度值,J1,J2为两点的经度值 )
推导过程就不写了,网上可以查到很明确的推导过程。
然后算出了球面距离,其实就是一段弧,根据弧长求弦长:
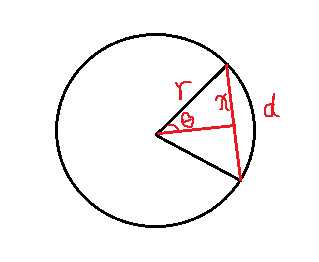
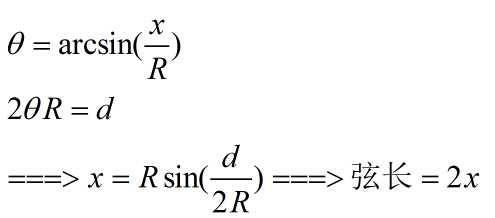
代码:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define pi acos(-1.0)
using namespace std;
int main()
{
int t,n,i;
double x1,x2,y1,y2;
double R = 6371009;
scanf("%d",&t);
while(t--)
{
scanf("%lf%lf",&x1,&y1);
scanf("%lf%lf",&x2,&y2);
x1 = x1*pi/180.0;
y1 = y1*pi/180.0;
x2 = x2*pi/180.0;
y2 = y2*pi/180.0;
double ans = R*acos(sin(x1)*sin(x2)+cos(x1)*cos(x2)*cos(y1-y2));
printf("%.0f\n",ans-2*R*sin(ans/(2*R)));
}
return 0;
}
UVA 11817 Tunnelling the Earth --球面距离公式
原文:http://www.cnblogs.com/whatbeg/p/4160447.html