考虑一个代价函数C , 它根据参数向量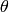 计算出当前迭代模型的代价,记作C(
计算出当前迭代模型的代价,记作C(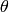 ).
机器学习中,我们的任务就是得到代价的最小值,在机器学习中代价函数通常是损失函数的均值,或者是它的数学期望。见下图:
).
机器学习中,我们的任务就是得到代价的最小值,在机器学习中代价函数通常是损失函数的均值,或者是它的数学期望。见下图:
这个叫做泛化损失,在监督学过程中,我们知道z=(x,y) ,并且 f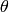 (x)
是对y的预测。
(x)
是对y的预测。
什么是这里的梯度呢?
当 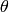 是标量的时候,代价函数的梯度可表示如下:
是标量的时候,代价函数的梯度可表示如下:
当 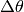 很小的时候,它就是
很小的时候,它就是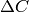 的另外一种表达,而我们就是让
的另外一种表达,而我们就是让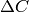 小于零,且越小越好。
小于零,且越小越好。
当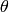 时一个向量的时候,代价函数的
梯度也是一个向量,每个都是一个
时一个向量的时候,代价函数的
梯度也是一个向量,每个都是一个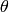 i,这里我考虑其他变量是固定的,仅仅是
i,这里我考虑其他变量是固定的,仅仅是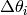 在变化。当
在变化。当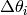 很小的时候,
很小的时候, 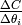 就成为
就成为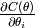
再来看梯度下降:
这里我们的目标是找到一个能够最小化代价函数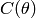 的
的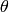 。若果我们能够搞定这个式子,我们就牛叉大了
。若果我们能够搞定这个式子,我们就牛叉大了
这样我们就找到最优的模型了。然而理想很丰满,现实很骨感,在99.99999%的情况下,我们不可能找到上面那个等式的答案,除非计算机是人,所以我们使用数学优化方法。大部分方法就是本地下降的想法。
每轮迭代调整下 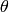 ,去减少代价函数的值,直到不能下降代价函数为止,这样我们达到了一个本地最小值(如果我们很幸运,我可能找到的就是全局最小值)。
,去减少代价函数的值,直到不能下降代价函数为止,这样我们达到了一个本地最小值(如果我们很幸运,我可能找到的就是全局最小值)。
最简单的基于梯度的优化技术就是梯度下降。有很多梯度下降的方法,我们这里说的是最普通的方法。
这里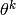 代表第K论的迭代,
代表第K论的迭代, 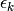 就是学习率,它是个标量。你可以使用固定的学习率,也可以使用适配的学习率,此处不再详表。
就是学习率,它是个标量。你可以使用固定的学习率,也可以使用适配的学习率,此处不再详表。
我们再来看一个随机梯度下降法(Stochastic Gradient Descent),简称SGD:
我们知道C是个均值,一般和具体的样本无关,如果我们对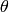 的更新更快一点,在极端情况下,每个样本更新一次,我们有下面的公式:
的更新更快一点,在极端情况下,每个样本更新一次,我们有下面的公式:
,这里Z是下一个样本,或者是在线学习的下一个输入信号。SGD是一个更加通用的原则,它的梯度下降方向比较随机,换句话说,是随着兴趣的方向下降的。SGD和普通的梯度下降基本类似,只不过它增加了不少随机性。
SGD比普通的梯度下降(批量梯度下降)更快,因为它更新权值向量更频繁。这个对于数据集比较大的时候,或者是在线学习比较有用。事实上,在机器学习任务中,大家仅仅在代价函数无法分解为上面的式子的时候才使用批量梯度下降法。
小批量梯度下降法:
这个不想仔细讲了,就是说每训练10个或者20个下降一次,方法和批的那个差不多。
移动均线法法:
我们不使用当前的样本的梯度,而是计算一个过去样本的移动均线,然后用移动均线去做权值向量的调整。
-------------------------------最后华丽的分割线------------------------------------------
本教程的目录博文请点击这里。
如果大家想先对机器学习进行入门了解,可参看这里的简单介绍。如果需要简单了解深度学习的内容,可参看这里简单的介绍。学习这些教程之前,可以先热身下,这里是theano的基础教程,学完之后,再看下这个东东,里面有一些基本的概念和一些测试的训练集。
原文:http://blog.csdn.net/rodneyzhaonet/article/details/41987089