这道题和求字段和的要求就差一点,就是那个是一条链, 这个是个环,关于这么环,刚开始按照链那种方式推倒状态转移方程,但是没有写出来,后来看题解,才看到原来还是转化为普通的单链来做,好多题都是由不会的转化成简单的来做的。还得多思考啊,碰见题就不想动脑子,真是什么都学不了啊
思路:一共有2种,首先是求单链最大值(也就是首尾不相接),这种普通的dp就能求出来,还有就是求单链最小值,用总和减去这个即为除了第一种情况之外的,记住,除了第一种情况能求出来的之外的最大值,刚开始我就是卡到这里了,明明第二种我能找到反例,为什么对呢,后来发现还有一个第一种情况呢,所以最后要比较他们当中谁更大些,选取更大的一个
下面的图示帮忙理解最大值的四种情况。
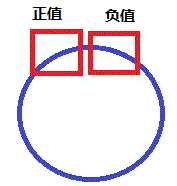
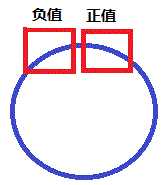
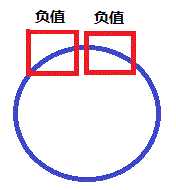
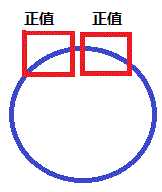
第一种 第二种 第三种 第四种
前三种情况都可以用单链的方式求出来,因为就选首尾相接了,也不是最大的,所以前三种情况是第一种,最后一种就是这道题的根本,就像样例第一组数据,3 ,-1, 2,构成最大的在两头,所以这时候要用第二种方法,用第一种求出来的最大值不是最大的,但是求出来的最小值一定是最小的,所以,总的减去最小的,就是最大的,这样这个题就变得简单了
代码如下:
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 using namespace std; 6 const long long INF = 999999999999999; 7 const int N = 50000 + 10; 8 int a[N]; 9 long long min_num, max_num;//保存字段和的最大值与最小值 10 int main() 11 { 12 int n; 13 while (~scanf("%d", &n)) 14 { 15 min_num = INF;//初始化 16 max_num = -INF; 17 long long t1 = 0, t2 = 0; 18 long long sum = 0; 19 for (int i = 0; i < n; i++) 20 { 21 scanf("%lld", &a[i]); 22 sum += a[i]; 23 if (t1 > 0) 24 t1 += a[i]; 25 else 26 t1 = a[i]; 27 if (t1 > max_num) 28 max_num = t1; 29 if (t2 < 0) 30 t2 += a[i]; 31 else 32 t2 = a[i]; 33 if (t2 < min_num) 34 min_num = t2; 35 } 36 if (max_num < sum - min_num) 37 max_num = sum - min_num; 38 printf("%lld\n", max_num); 39 } 40 return 0; 41 }
原文:http://www.cnblogs.com/Howe-Young/p/4173913.html