CF232 D2D：On Sum of Fractions，math

题目：http://codeforces.com/contest/397/problem/D

关键是要用数学归纳法证明：当n + 1 = p, p 为质数时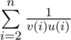， = 1 / 2 - 1 / p。

证明过程：当p = 3时，显然成立，假设q为下一个质数，则 原式 = 1 / 2 - 1 / p + (q - p) / (p*q) = 1/2 - 1/q。得证。

代码：

#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <iostream>
#include <sstream>
#include <iomanip>

#include <bitset>
#include <string>
#include <vector>
#include <stack>
#include <deque>
#include <queue>
#include <set>
#include <map>

#include <cstdio>
#include <cstdlib>
#include <cctype>
#include <cmath>
#include <cstring>
#include <ctime>
#include <climits>

using namespace std;
typedef pair<int, int> pii;
typedef long long llong;
typedef pair<llong, llong> pll;
#define mkp make_pair

#define CHECKTIME() printf("%.2lf\n", (double)clock() / CLOCKS_PER_SEC)

const int MOD = 1e9 + 7;

bool isPrime(long long n)
{
	int lim = floor( sqrt(n * 1.0 + 0.5) );
	for (int i = 2; i <= lim; i++) {
		if (n % i == 0) {
			return false;
		}
	}
	return true;
}
long long gcd(long long a, long long b)
{
	if (a < b) {
		swap(a, b);
	}
	while (b != 0) {
		long long t = a % b;
		a = b;
		b = t;
	}
	return a;
}
int main()
{
#ifdef LOCAL_DEBUG
	freopen("in.txt", "r", stdin);
#endif
	int t, n;
	cin >> t;
	for (int i = 0; i < t; i++) {
		cin >> n;
		long long p, q;
		p = n + 1;
		while (!isPrime(p)) {
			--p;
		}
		q = n + 1;
		while (!isPrime(q)) {
			++q;
		}
		// 1/2 - 1/p + (n - p + 1) * 1/(p * q)
		long long t1 = p * q - 2 * q + 2 * (n - p + 1);
		long long t2 = 2 * p * q;
		long long g = gcd(t1, t2);
		cout << t1 / g << "/" << t2 / g << endl;
	}
	

	return 0;
}

CF232 D2D：On Sum of Fractions，math,布布扣,bubuko.com

CF232 D2D：On Sum of Fractions，math

原文：http://blog.csdn.net/xzz_hust/article/details/20222049