在开始这个系列之前,首先说说什么是redis。redis是一个ANSI C编写的高性能Key-Value内存数据库,也是现在nosql数据库的代表之一。通过对redis2.8.17代码行数进行了统计,包括注释总共大约5万行,在开源家族里面算是非常短小精悍了,而且项目从2009年开始,距离现在很近,代码风格也非常适合我们80,90后程序员的知识结构。当具备一定编码经验之后,优秀的源码是我们最好的老师,尤其是已经被实践验证了的代码。特别由于最近正在苦读APUE和UNP,读到许多东西还是感到疑惑,而这种疑惑我感觉更应该到实际的代码中找答案。
网上各种关于redis的源码分析博文已算是海量了,但作为以学习目的在unix/linux c中的菜鸟,笔者更喜欢先从代码模块本身自低向上分析redis,尤其注重去学习其优秀的代码片段。好了,闲话少说,先从今天看到的一个小模块rand来开始。对于有一定c语言编程经验的程序员来说,rand是一个内在功能,ANSI C提供了关于rand和srand实现。那为什么redis还要做重复造轮子的活动呢?
/* Pseudo random number generation functions derived from the drand48() * function obtained from pysam source code. * * This functions are used in order to replace the default math.random() * Lua implementation with something having exactly the same behavior * across different systems (by default Lua uses libc's rand() that is not * required to implement a specific PRNG generating the same sequence * in different systems if seeded with the same integer). * * The original code appears to be under the public domain. * I modified it removing the non needed functions and all the * 1960-style C coding stuff... * * ----------------------------------------------------------------------------这是关rand.c前面的注释,这里我们可以看到两个内容。第一,作者认为不同的系统中实现math.random的方式不一样,由此作者使用了这一个模块代替系统中rand的实现方式,第二,它也不是redis的原生的模块,而是来自一个pysam项目。不过对于我们来说也先不在乎它到底为了什么,还是从哪里来,而更简单地看看它是如何实现的。rand采用的算法叫drand48,为什么是drand48,是因为它使用的是48bit的空间一种线性同余算法。那什么又是线性同余算法?我们看看维基百科的解释
线性同余方法(LCG)是个产生伪随机数的方法。
它是根据递归公式:
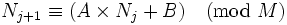
其中 是产生器设定的常数。
是产生器设定的常数。
LCG的周期最大为 ,但大部分情况都会少于M。要令LCG达到最大周期,应符合以下条件:
,但大部分情况都会少于M。要令LCG达到最大周期,应符合以下条件:
#include <stdint.h>
#define N 16
#define MASK ((1 << (N - 1)) + (1 << (N - 1)) - 1)
#define LOW(x) ((unsigned)(x) & MASK)
#define HIGH(x) LOW((x) >> N)
#define MUL(x, y, z) { int32_t l = (long)(x) * (long)(y); (z)[0] = LOW(l); (z)[1] = HIGH(l); }
#define CARRY(x, y) ((int32_t)(x) + (long)(y) > MASK)
#define ADDEQU(x, y, z) (z = CARRY(x, (y)), x = LOW(x + (y)))
#define X0 0x330E
#define X1 0xABCD
#define X2 0x1234
#define A0 0xE66D
#define A1 0xDEEC
#define A2 0x5
#define C 0xB
#define SET3(x, x0, x1, x2) ((x)[0] = (x0), (x)[1] = (x1), (x)[2] = (x2))
#define SETLOW(x, y, n) SET3(x, LOW((y)[n]), LOW((y)[(n)+1]), LOW((y)[(n)+2]))
#define SEED(x0, x1, x2) (SET3(x, x0, x1, x2), SET3(a, A0, A1, A2), c = C)
#define REST(v) for (i = 0; i < 3; i++) { xsubi[i] = x[i]; x[i] = temp[i]; } return (v);
#define HI_BIT (1L << (2 * N - 1))
static uint32_t x[3] = { X0, X1, X2 }, a[3] = { A0, A1, A2 }, c = C;
static void next(void);
int32_t redisLrand48() {
next();
return (((int32_t)x[2] << (N - 1)) + (x[1] >> 1));
}
void redisSrand48(int32_t seedval) {
SEED(X0, LOW(seedval), HIGH(seedval));
}
static void next(void) {
uint32_t p[2], q[2], r[2], carry0, carry1;
MUL(a[0], x[0], p);
ADDEQU(p[0], c, carry0);
ADDEQU(p[1], carry0, carry1);
MUL(a[0], x[1], q);
ADDEQU(p[1], q[0], carry0);
MUL(a[1], x[0], r);
x[2] = LOW(carry0 + carry1 + CARRY(p[1], r[0]) + q[1] + r[1] +
a[0] * x[2] + a[1] * x[1] + a[2] * x[0]);
x[1] = LOW(p[1] + r[0]);
x[0] = LOW(p[0]);
}
首先,我们发现好像比我们想的要复杂的多。每个数按照16位为一个单位被分到了一个长度为三的数组中,而其四则运算也发生了改变,通过定义MUL来表示乘法,ADDEQU来表示加法,LOW表示取低16位,HIGH表示取高十六位,CARRAY来判断是否有进位发生。从而实现了与一句表达式相同的功能。这时我们心中有疑问why,我们试着解读边界条件,由于用到48bit的结果,而实际运算结果更是超出48bit,比如A就为36bit,如果n为48bit则总公可能产生的为84bit,甚至超出了long long的范围。而采用数组的方式实现四则运算则不会出现这一问题。代码中大量使用了宏函数和位运算,在此实现中我们可以看到这些技巧是C程序设计中处理数值类问题的利器,值得借鉴和学习。原文:http://blog.csdn.net/kaixin89/article/details/42175457