解题思路:题目给出的描述就是一种求最长上升子序列的方法 将该列数an与其按升序排好序后的an‘求出最长公共子序列就是最长上升子序列
但是这道题用这种方法是会超时的,用滚动数组优化也超时,
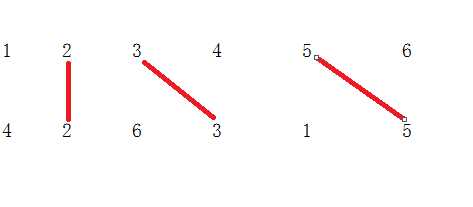
下面是网上找的求LIS的算法
假设要寻找最长上升子序列的序列是a[n],然后寻找到的递增子序列放入到数组b中。
(1)当遍历到数组a的第一个元素的时候,就将这个元素放入到b数组中,以后遍历到的元素都和已经放入到b数组中的元素进行比较;
(2)如果比b数组中的每个元素都大,则将该元素插入到b数组的最后一个元素,并且b数组的长度要加1;
(3)如果比b数组中最后一个元素小,就要运用二分法进行查找,查找出第一个比该元素大的最小的元素,然后将其替换。
在这个过程中,只重复执行这两步就可以了,最后b数组的长度就是最长的上升子序列长度。
例如样例给的 4 2 6 3 1 5
那么
4//
2//用2替换4
2 6//加入6
2 3//用3替换6
1 3//用1替换2
1 3 5//加入5
注意最后得到的a数组中的数为1 3 5
而实际上我们要求的最长上升序列为 2 3 5 但是我们只需要求长度,所以不影响
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 736 Accepted Submission(s): 486
 Figure 1. To the left: The two blocks‘ ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.
Figure 1. To the left: The two blocks‘ ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged. #include<stdio.h>
int b[500010],f[500010];
int bserch(int f[],int n,int v)
{
int x,y,m;
x=1;
y=n;
while(x<=y)
{
m=(x+y)/2;
if(v>=f[m])
x=m+1;
else
y=m-1;
}
return x;
}
int main()
{
int i, n,len,ncase,tmp,x,y;
scanf("%d",&ncase);
while(ncase--)
{
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&b[i]);
len=1;
f[1]=b[1];
for(i=2;i<=n;i++)
{
if(b[i]>=f[len])
{
len++;
f[len]=b[i];
}
else
{
tmp=bserch(f,len,b[i]);
f[tmp]=b[i];
}
}
printf("%d\n",len);
}
}
HDU 1950 Bridging signals【最长上升序列】
原文:http://www.cnblogs.com/wuyuewoniu/p/4210769.html