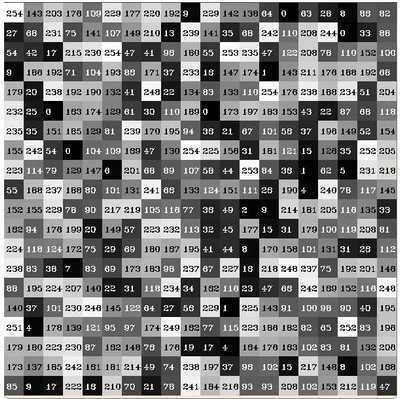
直方图可以统计的不仅仅是颜色灰度, 它可以统计任何图像特征 (如 梯度, 方向等等)。直方图的一些具体细节:
怎样去统计两个特征呢? 在这种情况下, 直方图就是3维的了,x轴和y轴分别代表一个特征, z轴是掉入 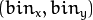 组合中的样本数目。OpenCV提供了一个简单的计算数组集(通常是图像或分割后的通道)的直方图函数 calcHist 。
支持高达 32 维的直方图。
组合中的样本数目。OpenCV提供了一个简单的计算数组集(通常是图像或分割后的通道)的直方图函数 calcHist 。
支持高达 32 维的直方图。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 |
/// 分割成3个单通道图像 ( R, G 和 B )vector<Mat> rgb_planes;split( src, rgb_planes );/// 设定bin数目int histSize = 255;/// 设定取值范围 ( R,G,B) )float
range[] = { 0, 255 } ;const
float* histRange = { range };bool
uniform = true; bool
accumulate = false;/// 计算直方图:calcHist( &rgb_planes[0], 1, 0, Mat(), r_hist, 1, &histSize, &histRange, uniform, accumulate ); |
在画直方图之前,先使用 normalize 归一化直方图,这样直方图bin中的值就被缩放到指定范围(这个步骤只是为了让直方图的值可以显示在目标窗口中):
|
1
2 |
/// 将直方图归一化到范围 [ 0, histImage.rows ]normalize(r_hist, r_hist, 0, histImage.rows, NORM_MINMAX, -1, Mat() ); |
画出直方图也有一些小技巧(窗口上方y轴坐标为0,向下增长):
|
1
2
3
4
5
6
7 |
/// 在直方图画布上画出直方图for( int
i = 1; i < histSize; i++ ){ line( histImage, Point( bin_w*(i-1), hist_h - cvRound(r_hist.at<float>(i-1)) ) , Point( bin_w*(i), hist_h - cvRound(r_hist.at<float>(i)) ), Scalar( 0, 0, 255), 2, 8, 0 );} |
以上。
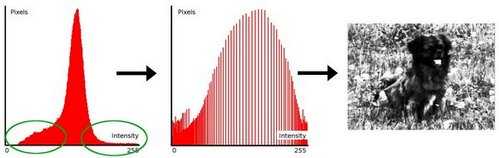
直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法.
注意:只能对单通道进行均衡化。
|
1 |
equalizeHist( src, dst ); |
要想实现均衡化的效果, 映射函数应该是一个 累积分布函数 (cdf) (更多细节,
参考*学习OpenCV*). 对于直方图 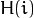 ,
它的 累积分布
,
它的 累积分布 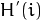 是:
是:
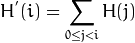
要使用其作为映射函数, 我们必须对最大值为255 (或者用图像的最大强度值) 的累积分布 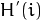 进行归一化.
同上例, 累积分布函数为:
进行归一化.
同上例, 累积分布函数为:
最后, 我们使用一个简单的映射过程来获得均衡化后像素的强度值: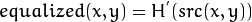
详细映射过程
OpenCV 函数 compareHist 执行了具体的直方图对比的任务。该函数提供了4种对比标准来计算相似度:
Correlation ( CV_COMP_CORREL )
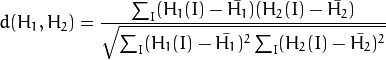
其中
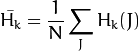
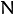 是直方图中bin的数目。
是直方图中bin的数目。
Chi-Square ( CV_COMP_CHISQR )
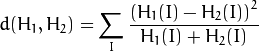
Intersection ( CV_COMP_INTERSECT )
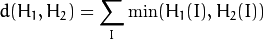
Bhattacharyya 距离( CV_COMP_BHATTACHARYYA )
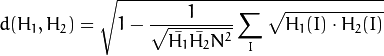
|
1 |
double
base_test1 = compareHist( hist_base, hist_test1, compare_method ); |
对于 Correlation 和 Intersection 标准, 值越大相似度越大。而另外两种对比标准,则是结果越小相似度越大。
反向投影是一种记录给定图像中的像素点如何适应直方图模型像素分布的方式。所谓反向投影就是首先计算某一特征的直方图模型,然后使用模型去寻找图像中存在的该特征。其步骤为:
对测试图像中的每个像素 ( 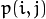 ),获取色调数据并找到该色调(
),获取色调数据并找到该色调( 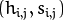 )在直方图中的bin的位置。
)在直方图中的bin的位置。
查询 模型直方图 中对应的bin - 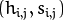 -
并读取该bin的数值。
-
并读取该bin的数值。
将此数值储存在新的图像中(BackProjection)。 你也可以先归一化 模型直方图 ,这样测试图像的输出就可以在屏幕显示了。
通过对测试图像中的每个像素采用以上步骤, 我们得到了下面的 BackProjection 结果图:
例如,假如源图像是一张 肤色图,那么测试图像中亮色区域表示其更有可能属于皮肤区域(因为其对应的模型直方图值很高)。
调用函数 calcBackProject 计算图像的反向投影,示例见此。
OpenCV学习笔记(十) 直方图操作,布布扣,bubuko.com
原文:http://www.cnblogs.com/ericxing/p/3580377.html