题意是给定k(k=3,5,6),a,问是否存在一个四边形数,使得它的a倍是一个k边形数。如果存在,求出最小解
k边形数的定义
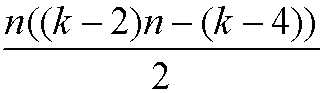
那么题目意思实际是求解关于x,y的不定方程
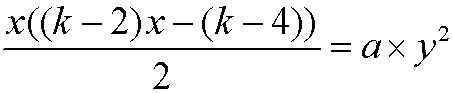
代入具体的k并变形可以得到
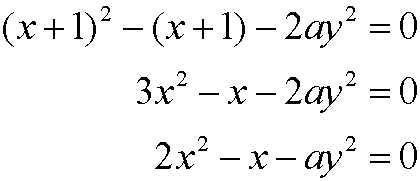
可以看出这几个方程具有相同的形式,我们考虑更一般的情况
![]()
配方可以得到
![]()
换元可以得到关于z,y的不定方程
![]()
显然这是一个佩尔方程,当4ab为完全平方数无解,否则有无数组正整数解
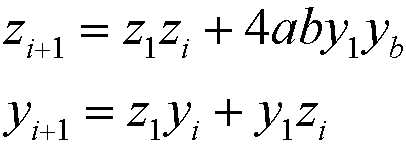
其中![]() 为方程的最小解。显然有
为方程的最小解。显然有
![]()
那么问题可以转化为找到一个最小的n,使得
![]()
这个一般化问题我也不知道怎么做。。只会暴力
不过本题中a只取到1,2,3,这个时候n若存在,必为1,因此只要测试z1是否符合答案即可。(可以枚举z1%2a得到这个结论)

1 bint h[2] ,k[2] ; 2 void Solve( int n ){ 3 ll c ,q ,a ,step = 0 ,sqrtn = sqrt(n+.0) ; 4 c = sqrtn ,q = n - c * c ,a = ( sqrtn + c ) / q ; 5 ll bc = c ,bq = q ; 6 h[0] = 1 ,h[1] = sqrtn ; 7 k[0] = 0 ,k[1] = 1 ; 8 while( 1 ){ 9 h[step] = a * h[step^1] + h[step] ; 10 k[step] = a * k[step^1] + k[step] ; 11 c = a * q - c ; 12 q = ( n - c * c ) / q ; 13 a = ( sqrtn + c ) / q ; 14 if( c == bc && q == bq && step ) return ; 15 step ^= 1 ; 16 } 17 }
ZOJ 3759 几个二元二次不定方程的解法,布布扣,bubuko.com
原文:http://www.cnblogs.com/MyWither/p/3580551.html