这个博主找规律的部分写得很好,原样放在下面。最后给出了顺时针和逆时针方向的螺旋队列的实现,可以看出它们的差别如此之小。
和螺旋队列类似,也是找规律的zigzag数组见这个帖子。
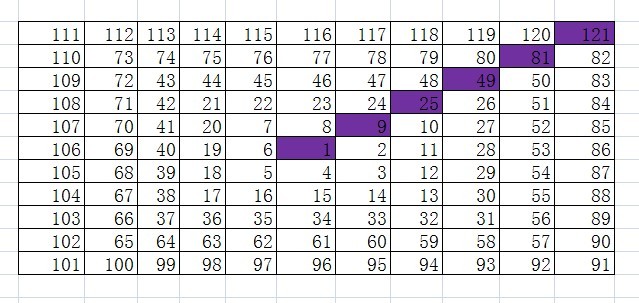
1、螺旋规律
2、奇数(圈数,或X轴正坐标)平方规律(紫线)
设1的坐标是(0,0),x方向向右为正,y方向向下为正,例如,7的坐标为(-1,-1),2的坐标为(1,0)。编程实现输入任意一点坐标(x,y),输出所对应的数字!
从紫线突破。
从图中不难发现,每圈最大值max=(2*c+1)(2*c+1),c为由内往外的圈数,c>=0。如图每圈最大值分别是1、9、25、49、81........,算出每圈的max后,就分4条边分别计算每圈的其他值。通过坐标落在该圈4条边的哪条边上,按照不同的公式计算出具体坐标点的值。
以第3圈(max=49)为例,4条边划分如下图(以颜色区分):

这里先给出4条边上各坐标上的值与max的对应关系为:
上边:Utop = max+(x+y);
左边: Uleft= max+(3*x-y);
下边:Ubottom = max + (-x - 5*y);
右边:Uright = max+(-7*x+y);
那么这些关系是怎么得出来的呢?再看图中画上圈的数字(将其值表示为topBase,xxBase),我们称其为每条边的基准值:
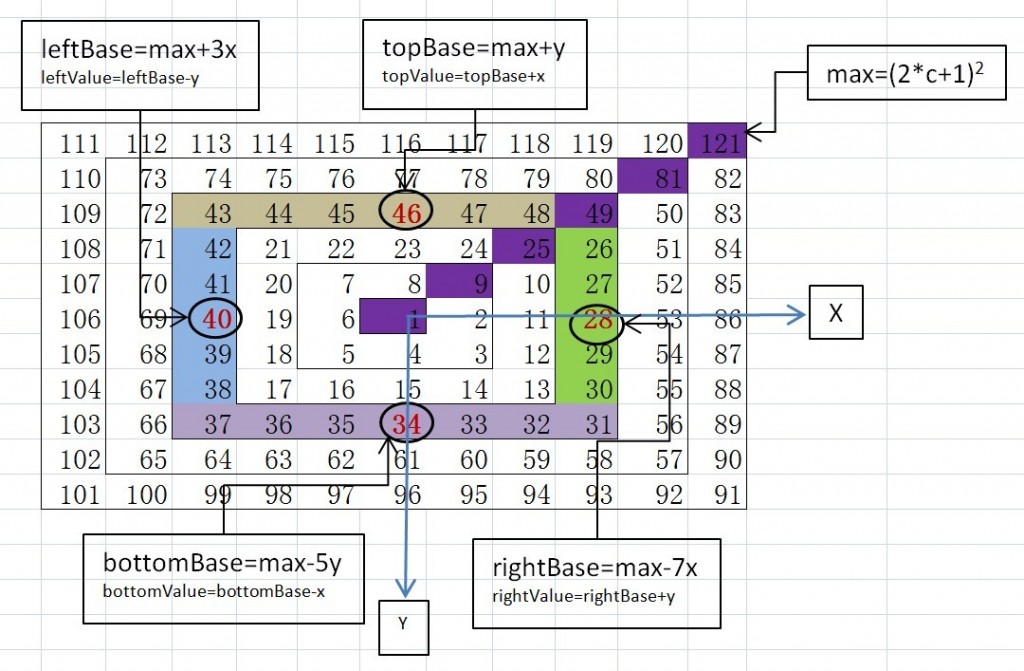
观察这些基准值与max值之间关系,不难发现,这些基准值与max之间的差分别是1C(上边),3C(左边),5C(下边),7C(右边)(C表示当前圈数),在上边和下边,y坐标表示(或等于)圈数(即C=y),而在左边和右边,x坐标表示(或等于)圈数(即C=x)。因此前面提到的差值又可用坐标表示成1y,3x,5y,7x。因此就产生了各边基准值的计算公式:
topBase=max+y
leftBase=max+3x
bottomBase=max-5y
rightBase=max-7x
(注意坐标的符号,负数加,正数减,因为基准值肯定都比max要小)下面得出每条边的值,首先考虑上边和下边,这2条边,在基准值的基础上,由x坐标控制增减,因此:
topValue=topBase+x=max+y+x(上边,随x赠而赠,因此是加x)
bottomValue=bottomBase-x=max-5y-x(下边,随x赠而减,因此是减x)
同理,左边和右边,则在基准值的基础上,由y坐标控制增减,因此:
leftValue=leftBase-y=max+3x-y(左边,随y赠而减,因此是减y)
rightValue=rightBase+y=max-7x+y(右边,随y赠而赠,因此是加y)
int abs(int a) {
return a >= 0 ? a : -a;
}
int MaxValue(int a, int b) {
return a > b ? a : b;
}
int Spiral(int x, int y) {
int c = MaxValue(abs(x), abs(y));
int max = (c * 2 + 1)*(c * 2 + 1);
if (y == -c) //上方
return max + (x + y);
else if (x == -c) //左边
return max + (3 * x - y);
else if (y == c) //下边
return max + (-x - 5 * y);
else //右边
return max + (-7 * x + y);
}
int main() {
int i, j;
printf("顺时针:\n");
for (i = -4; i <= 4; i++) {
for (j = -4; j <= 4; j++) {
printf("%5d", Spiral(j, i)); //注释A
}
printf("\n");
}
printf("\n");
printf("----------------------------------------\n");
printf("逆时针:\n");
for (i = -4; i <= 4; i++) {
for (j = -4; j <= 4; j++) {
printf("%5d", Spiral(i, j)); //注释B }
printf("\n");
}
}该程序的执行结果如下图所示。
可以看出,在main函数中仅仅交换了注释A、B处的i和j就使得输出的螺旋队列分别是顺时针方向和逆时针方向。
原文:http://blog.csdn.net/u013074465/article/details/43157737