在写题解之前给自己打一下广告哈~。。抱歉了，希望大家多多支持我在CSDN的视频课程，地址如下：

http://edu.csdn.net/course/detail/209

题目：

骨牌铺方格

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 744 Accepted Submission(s): 478

Problem Description 在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：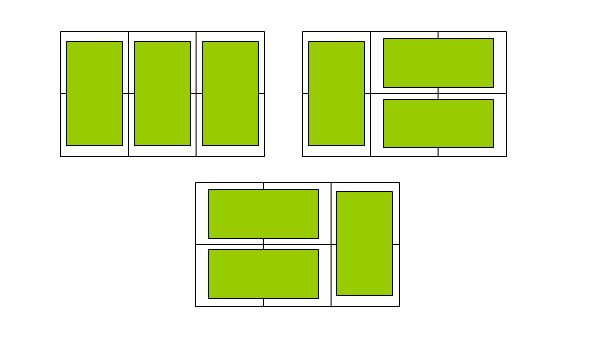

Input 输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

Output             对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

Sample Input 1 3 2

Sample Output 1 3 2

Author lcy

Source 递推求解专题练习（For Beginner）

Recommend lcy

题目分析：

            简单递推。假设dp[i]为铺满2*n网格的方案数.那么dp[i]=dp[i-1]+dp[i-2]。其中dp[i-1]为铺满2*(n-1)网格的方案数(既然前面的2*(n-1)的网格一已经铺满,那么最后一个只能是竖着放)。dp[i-2]为铺满2*(n-2)网格的方案数(如果前面的2*(n-2)的网格已经铺满,那么最后的只能是横着放,否则会重复).其实这种递推题，在独立思考得到递推公式后,其实可以将输入样例带进去验证一下.需要注意的是dp[50]已经到200多亿了，这时候需要用long long 。

代码如下：

/*
 * b.cpp
 *
 *  Created on: 2015年2月5日
 *      Author: Administrator
 */

#include <iostream>
#include <cstdio>

using namespace std;

const int maxn = 52;

long long dp[maxn];



void prepare(){
	dp[1] = 1;
	dp[2] = 2;

	int i;
	for(i = 3 ; i < maxn ; ++i){
		dp[i] = dp[i-1] + dp[i-2];
	}
}

int main(){
	prepare();
	int n;
	while(scanf("%d",&n)!=EOF){
		printf("%lld\n",dp[n]);
	}

	return 0;
}

(hdu step 3.1.2)骨牌铺方格(简单递推：求用2*1的骨牌铺满2*n的网格的方案数)

原文：http://blog.csdn.net/hjd_love_zzt/article/details/43526243