http://acm.hdu.edu.cn/showproblem.php?pid=4328
2 1 1 B 3 3 BBR RBB BBB
Case #1: 4 Case #2: 8
/**
hdu4328 最大子矩阵问题O(n*m)
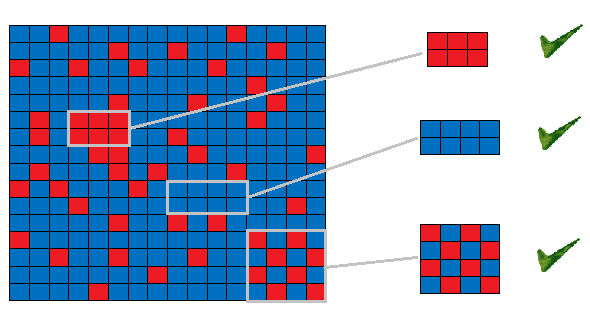
题目大意:给定一个n*m的棋盘有红黑两色,让截取一个周长最大矩形,该矩形要么全是黑色,要么全是红色,要么黑色和红色交替
见题目附图。
解题思路:如果遍历每一个矩阵是不可能的,时间O(n*n*n),因此我们采用扫描的方法(白书P51)。对于交替的矩形我们把(i+j)
为奇数的格子翻转颜色,那样就可以转换成全是一样颜色了,然后边成把(i+j)为偶数的翻转,四种情况取最大即可。复杂度O(n*m)
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
const int maxn=1005;
int mat[maxn][maxn],mat1[maxn][maxn],up[maxn][maxn],lef[maxn][maxn],rig[maxn][maxn];
char a[maxn][maxn];
int n,m;
int get()
{
int ans=0;
for(int i=0; i<m; i++)
{
int lo=-1,ro=n;
for(int j=0; j<n; j++)
{
if(mat[i][j]==1)
{
up[i][j]=lef[i][j]=0;
lo=j;
}
else
{
up[i][j]=i==0?1:up[i-1][j]+1;
lef[i][j]=i==0?lo+1:max(lef[i-1][j],lo+1);
}
}
for(int j=n-1; j>=0; j--)
{
if(mat[i][j]==1)
{
rig[i][j]=n;
ro=j;
}
else
{
rig[i][j]=i==0?ro-1:min(rig[i-1][j],ro-1);
ans=max(ans,up[i][j]*2+2*(rig[i][j]-lef[i][j]+1));
}
}
}
return ans;
}
int main()
{
int tt=0,T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&m,&n);
for(int i=0; i<m; i++)
{
scanf("%s",a[i]);
}
for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
if(a[i][j]=='R')
mat1[i][j]=mat[i][j]=1;
else
mat1[i][j]=mat[i][j]=0;
}
}
int ans=-1;
///1
ans=max(ans,get());
///2
for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
if(mat1[i][j]==1)
mat[i][j]=0;
else
mat[i][j]=1;
}
}
ans=max(ans,get());
///3
for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
if((i+j)%2==1)
{
if(mat1[i][j]==1)
mat[i][j]=0;
else
mat[i][j]=1;
}
else
mat[i][j]=mat1[i][j];
}
}
/* for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
printf("%d",mat[i][j]);
}
printf("\n");
}
printf("\n");*/
ans=max(ans,get());
///4
for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
if((i+j)%2==0)
{
if(mat1[i][j]==1)
mat[i][j]=0;
else
mat[i][j]=1;
}
else
mat[i][j]=mat1[i][j];
}
}
/*for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
printf("%d",mat[i][j]);
}
printf("\n");
}
printf("\n");*/
ans=max(ans,get());
printf("Case #%d: %d\n",++tt,ans);
}
return 0;
}
/**
100
3 3
BBR
RBR
BBB
2 2
BR
RB
2 2
BB
RR
2 2
BB
BB
*/原文:http://blog.csdn.net/lvshubao1314/article/details/43560963