一、 树

1. 树的定义

　　树结构是一种非常重要的非线性结构，该结构中的一个数据元素可以有两个或两个以上的直接后继元素；它是n(n>=0)个结点的有限集合，当n=0时称为空树。在任意飞空树中有且仅有一个称为根的结点；

　　树的基本概念

　　a. 双亲、孩子和兄弟。结点的子树的根称为该结点的孩子，该结点称为其子结点的双亲（parent）。具有相同双亲的结点互为兄弟。

　　b. 结点的度。一个结点的子树的个数即为该结点的度。度数最大的结点的度称为树的度。

　　c. 叶子节点。度为0的节点，也称终端结点。

　　d. 内部结点。度不为0的节点（包括根节点），也称分支结点或非终端结点。除根节点以外，分值结点也称为内部结点。

　　e. 结点的层次。根为第一层，根的孩子为第二层，依此类推。

　　f. 树的高度。一棵树的最大层数记为树的高度（或深度）。

　　g. 有序（无序）树。若将树中结点的各子树看成是从左到右具有次序的，即不能交换，则称为改树为有序树，否则称为无序树。

2. 二叉树的定义

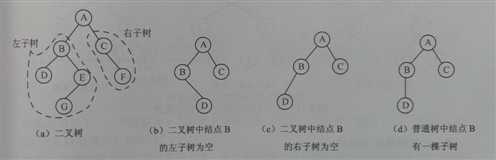
　　二叉树是n(n>=0)个结点的有限集合，它或者是空树（n=0），或者是由一个根节点及两棵不相交的且分别称为左、右子树的二叉树所组成。

树和二叉树的区别：

　　a. 二叉树中结点的子树要区分左子树和右子树，即使在结点只有一颗子树的情况下，也要明确指出该子树是左子树还是右子树。

　　b. 二叉树结点最大度为2，而树中不限制结点的度数。

　　二叉树的性质：

　　a. 二叉树第i层（i>=1）上最多有2^i-1个结点。

　　b. 高度为k的二叉树最多有2^k-1个结点（k>=1）。

　　c. 对于任何一颗二叉树，若其终端节点数为n₀，度为2的结点数为n₂，则n₀=n₂+1。

　　d. 具有n个结点的完全二叉树的深度为⌊log₂n⌋+1。（“⌊⌋”表示向下取整）

树结构

原文：http://www.cnblogs.com/ImaY/p/4276498.html