A Game
题意：A,B各自拥有两堆石子，数目分别为n1, n2，每次至少取1个，最多分别取k1,k2个, A先取，最后谁会赢。
分析：显然每次取一个是最优的，n1 > n2时，先手赢。
代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 using namespace std; 16 typedef long long LL; 17 typedef unsigned US; 18 typedef pair<int, int> PII; 19 typedef map<PII, int> MPS; 20 typedef MPS::iterator IT; 21 22 int main() { 23 // in 24 int n1, n2, k1, k2; 25 cin >> n1 >> n2 >> k1 >> k2; 26 puts(n1 > n2 ? "First" : "Second"); 27 28 29 30 31 return 0; 32 }
B1, B2 Permutations
题意：给定排列长度 n <= 50,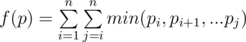 
,要求输出字典序第m大的排列,同时使得f(p)最大。
分析：
首先肯定的是应该从小到大，将每个数往剩余位置的两边放。反证法，如果将较小的放在中间，那么被各个区间包含的次数会比较多，结果会比较小，而将小的放在两边结果至少不会变小。
所以最多2^(n-1)个可能值，首先考虑1的放置，如果m > 2^(n-2)则放置在末尾，其他数同样考虑。
代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 using namespace std; 16 typedef long long LL; 17 typedef unsigned US; 18 typedef pair<int, int> PII; 19 typedef map<PII, int> MPS; 20 typedef MPS::iterator IT; 21 22 int main() { 23 24 vector<int> ans(55); 25 int n, m; 26 cin >> n >> m; 27 int l = 1, r = n; 28 for(int i = (n-1); i > 0; i--){ 29 if(m <= (1<<(i-1))) { 30 ans[l++] = n-i; 31 }else { 32 ans[r--] = n-i; 33 m -= (1<<(i-1)); 34 } 35 } 36 ans[l] = n; 37 for(int i = 1; i <= n; i++) 38 printf("%d ", ans[i]); 39 return 0; 40 }
C Second price auction
题意：n个区间(2 <= n <= 5), [Li, Ri](Ri <= 10000)，每个区间中随机选出一个整数，求第二大的数的数学期望。
分析：
比赛时做的比较复杂，但还是通过了。具体分为两种情况，最大值唯一和不唯一。
最大值唯一时：
用st表示此时除开最大值的是那些区间，然后dp[i][st]表示这些区间中最大值为i时的概率。
最大值不唯一：
只需要枚举那些区间为最大值，及最大值，计算期望即可。
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 using namespace std; 16 typedef long long LL; 17 typedef unsigned US; 18 typedef pair<int, int> PII; 19 typedef map<PII, int> MPS; 20 typedef MPS::iterator IT; 21 const int maxn = 10000 + 10; 22 23 double dp[maxn][(1<<5)+2]; 24 int L[10], R[10]; 25 int n; 26 double getProb(int st, int m) { 27 vector<int> comp; 28 for(int i = 0; i < n; i++) if(st&(1<<i)) 29 comp.pb(i); 30 int nn = sz(comp); 31 double res = 0.0; 32 for(int x = 1; x < (1<<nn); x++) { 33 // vector<int> tmp; 34 double tmpPro = 1.0; 35 int ok = 1; 36 for(int j = 0; j < nn; j++) if(x&(1<<j)) { 37 // tmp.pb(comp[j]); 38 // cout << L[comp[j]] << ‘ ‘ << R[comp[j]] << endl; 39 if(m < L[comp[j]] || m > R[comp[j]]) { 40 ok = 0; 41 // bug(1) 42 break; 43 } 44 tmpPro *= 1.0/(R[comp[j]]-L[comp[j]] + 1); 45 46 } else { 47 if(m <= L[comp[j]]) { 48 ok = 0; 49 break; 50 } 51 tmpPro *= 1.0*(min(R[comp[j]]+1, m)-L[comp[j]])/(R[comp[j]]-L[comp[j]] + 1); 52 } 53 if(ok) { 54 // cout << tmpPro << endl; 55 res += tmpPro; 56 } 57 } 58 return res; 59 } 60 int main() { 61 // in 62 cin >> n; 63 int mx = 0, mi = inf; 64 for(int i = 0; i < n; i++) { 65 cin >> L[i] >> R[i]; 66 mi = min(mi, L[i]); 67 mx = max(mx, R[i]); 68 } 69 for(int i = 1; i < (1<<n); i++) { 70 for(int j = mi; j <= mx; j++) 71 dp[j][i] = getProb(i, j); 72 } 73 // cout << getProb(5, 7) << endl; 74 // cout << dp[7][5] << endl; 75 double ans = 0.0; 76 int mask = (1<<n)-1; 77 for(int k = 0; k < n; k++) { 78 for(int l = mi; l < R[k]; l++) { 79 // if(k == 1) cout << l << ‘ ‘ << dp[l][mask^(1<<k)] << endl; 80 ans += dp[l][mask^(1<<k)]*l*(R[k]-max(L[k]-1, l))/(R[k]-L[k]+1); 81 } 82 } 83 // cout << ans << endl; 84 for(int i = mi; i <= mx; i++) { 85 for(int st = 1; st < (1<<n); st++) { 86 int ok = 1; 87 double tmp = 1.0; 88 for(int x = 0; x < n; x++) if((st&(1<<x))) { 89 // ct++; 90 if(i < L[x] || i > R[x]) { 91 ok = 0; 92 break; 93 } 94 tmp *= 1.0/(R[x]-L[x]+1); 95 } else { 96 if(i <= L[x]) { 97 ok = 0; 98 break; 99 } 100 tmp *= 1.0*(min(R[x]+1,i)-L[x])/(R[x]-L[x]+1); 101 } 102 if(ok && __builtin_popcount(st) >= 2) { 103 ans += tmp*i; 104 } 105 } 106 } 107 printf("%.12f\n", ans); 108 return 0; 109 }
D1, D2 Constrained Tree
题意：先序遍历的方式给二叉树标号，一些限制描述：ai bi LEFT or ai bi RIGHT表示bi位于ai的左子树或右子树，构造一棵满足条件的二叉树，中序遍历输出结点编号。
分析：对输入的描述处理，maxL[i]表示位于i结点左子树的点的最大编号，minR[i]，maxR[i]，表示i右子树结点最小和最大编号。
那么构造时，dfs(rt, must, no)记录rt为根的子树的3个信息，rt， must表示必须包含的点，no表示结点编号不能超过，对于根为rt的子树，其maxL[rt] < minR[rt]，并且当
进行构造时，要用maxR[rt]更新must。
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 using namespace std; 16 typedef long long LL; 17 typedef unsigned US; 18 typedef pair<int, int> PII; 19 typedef map<PII, int> MPS; 20 typedef MPS::iterator IT; 21 const int maxn = 1000000 + 10; 22 const int maxm = 100000 + 10; 23 int a[maxm], b[maxm], c[maxm]; 24 int maxL[maxn], maxR[maxn], minR[maxn]; 25 vector<int> ans; 26 int solve(int rt, int must, int no){ 27 if(must < maxR[rt]) 28 must = maxR[rt]; 29 if(must >= no) { 30 puts("IMPOSSIBLE"); 31 exit(0); 32 } 33 int last = rt; 34 if(maxL[rt]) 35 last = solve(rt+1, maxL[rt], minR[rt] ? minR[rt] : no); 36 if(!last) { 37 puts("IMPOSSIBLE"); 38 exit(0); 39 } 40 ans.pb(rt); 41 if(must >= last+1) 42 return solve(last+1, must, no); 43 return last; 44 } 45 int main(){ 46 // in 47 int n, m; 48 cin >> n >> m; 49 for(int i = 0; i < m; i++){ 50 static char s[10]; 51 scanf("%d%d%s", a+i, b+i, s); 52 if(s[0] == ‘L‘) maxL[a[i]] = max(maxL[a[i]], b[i]); 53 else { 54 maxR[a[i]] = max(maxR[a[i]], b[i]); 55 if(!minR[a[i]] || b[i] < minR[a[i]]) 56 minR[a[i]] = b[i]; 57 } 58 if(a[i] >= b[i] || (minR[a[i]] && maxL[a[i]] >= minR[a[i]])) 59 { 60 puts("IMPOSSIBLE"); 61 return 0; 62 } 63 } 64 solve(1, n, n+1); 65 for(int x: ans) 66 printf("%d ", x); 67 return 0; 68 }
E1, E2 Subarray Cuts
题意：一个长度为n的数组，依次选取连续的k部分（ k >= 2)，si表示第i部分的和，要求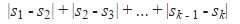 
最大。
分析：官方题解对于E1的解法用到了另一种结论，便是只需要考虑选取m个部分，m <= k， ( + s1 - 2·s2 + 2·s3 - 2·s4 + …) and ( - s1 + 2·s2 - 2·s3 + 2·s4 - …)的大小，且剩下的没有选取的元素>=k-m即可。采用dp即可解决，dp[i][sign][first][last][unused][max]， 表示从第i个元素开始，选取max个部分的最大值。
对于E2有另一种解法，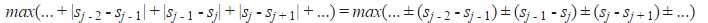
,
f(i, j, c1, c2) = max(... ± (sj -1 - sj -2)±c2(sj - sj - 1) ± c1 (0 - sj)...), 选取ai作为sj的一部分时，
f(i, j, c1, c2) = max(... ± (sj -1 - sj -2)±c2(sj - sj - 1) ± c1 (0 - sj)...)
= max(... ± (sj -1 - sj -2)±c2(0- sj - 1) ± c2sj+c1 (0 - sj)...)
= max(... ± (sj -1 - sj -2)±c2(0- sj - 1) ± (c2-c1)ai...) ，
f[c1][c2][k]表示从第i个往后选取sk时的最大值，g[c1][k] 表示max(f[c1][c2][k])，即当前选取sk后最大值，
更新时，f[c1][c2][k] = max(f[c1][c2][k], g[c1][k-1]) + (c2-c1)*a[k]。
虽然dp时没有确定各项前的符号，但是绝对值会是>=0, 因此最后得到最大值一定是将前面的c1, c2一定使得各项为>=0的，所以使能够得到最大值的。
题解看了不是很明白，上面的思路属于Petr的代码的，看了觉得理解了就将其按照理解写了一下。
代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 using namespace std; 16 typedef long long LL; 17 typedef unsigned US; 18 typedef pair<int, int> PII; 19 typedef map<PII, int> MPS; 20 typedef MPS::iterator IT; 21 const int maxn = 30000 + 10; 22 const int maxm = 200 + 10; 23 int a[maxn], f[2][2][maxm], g[2][maxm]; 24 int main() { 25 // inC 26 int n, k; 27 cin >> n >> k; 28 for (int i = 1; i <= n; i++) scanf("%d", a+i); 29 for(int i = 0; i < maxm; i++) for(int j = 0; j < 2; j++) { 30 g[j][i] = -inf; 31 for(int u = 0; u < 2; u++) 32 f[u][j][i] = -inf; 33 } 34 35 36 g[0][0] = g[1][0] = 0;//init by 0 37 for (int cur = 1; cur <= n; ++cur) { 38 for (int u = 1; u <= k; u++) 39 for (int now = 0; now < 2; now++) 40 for (int pre = 0; pre < 2; pre++) { 41 int e = (u == 1 ? 0 : 2*pre-1); 42 e += (u == k ? 0 : 1-2*now); 43 f[now][pre][u] = max(f[now][pre][u], g[pre][u-1]) + e*a[cur]; 44 } 45 for(int now = 0; now < 2; now++) 46 for(int u = 1; u <= k; u++) { 47 g[now][u] = max(g[now][u], max(f[now][0][u], f[now][1][u])); 48 } 49 } 50 printf("%d\n", max(g[0][k], g[1][k])); 51 return 0; 52 }
F1,F2 Scaygerboss
题意：males,female只雄蜂，雌蜂，及蜂王，位于一个n*m的迷宫，每只蜂可以移动到相邻位置上，时间为t，有障碍物的格子不能移动上去，要求能否每一只蜂和另外一只性别不同的蜂处于同一格子，且移动的最大时间最小。
分析：首先根据males和females的数目，将蜂王看做雌性或雄性（少的那一种），如果两种数目仍然不相等，则显然不会满足条件。
然后，构建网络流图，(src, sink)， src->males，容量为1，females-sink，容量为1，然后将每个空格子拆成两点，u,v,males->u, 及v->females表示占领该格子，u->v容量为1，当然为了求最小时间，需二分可能的时间，只有当males，females到相应格子时间<=二分值时才连相应的边，最大流的值 == males时表示可行。
代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 #define INF 0x0f0f0f0f0f0f0f0f 16 using namespace std; 17 typedef long long LL; 18 typedef unsigned US; 19 typedef pair<int, int> PII; 20 typedef map<PII, int> MPS; 21 typedef MPS::iterator IT; 22 23 const int maxn = 25; 24 const int maxm = 3000; 25 26 char maze[maxn][maxn]; 27 int g[maxn*maxn][maxn*maxn]; 28 int n, m, N, M; 29 int src, sink; 30 31 LL ans; 32 33 struct Node { 34 int r, c, t; 35 Node() {} 36 Node(int r, int c, int t):r(r), c(c), t(t) {} 37 }; 38 vector<Node> males, fmales; 39 40 struct Edge { 41 int u, v, c; 42 Edge() {} 43 Edge(int u, int v, int c):u(u), v(v), c(c) {} 44 }; 45 46 47 struct MaxFlow { 48 int n, m; 49 int Now[maxm], Dfn[maxm], Cur[maxm]; 50 51 vector<Edge> edges; 52 vector<int> G[maxm];//border ! 53 54 void init(int n) { 55 this->n = n; 56 for(auto &x: G) 57 x.clear(); 58 edges.clear(); 59 } 60 61 void add(int u, int v, int c) { 62 // cout << u << ‘-‘ << v << endl; 63 edges.pb(Edge(u, v, c)); 64 edges.pb(Edge(v, u, 0)); 65 m = sz(edges); 66 G[u].pb(m-2); 67 G[v].pb(m-1); 68 } 69 70 int ISAP(int s, int flow){ 71 if(s == sink) return flow; 72 int v, tab = n, now = 0, vary; 73 int p = Cur[s], &q = Cur[s]; 74 do{ 75 Edge &e = edges[G[s][q]]; 76 if(e.c > 0){ 77 if(Dfn[s] == Dfn[v = e.v] + 1) 78 vary = ISAP(v, min(flow-now, e.c)), now += vary, 79 e.c -= vary, edges[G[s][q]^1].c += vary; 80 if(Dfn[src] == n) return now; 81 if(e.c > 0) tab = min(tab, Dfn[v]); 82 83 } 84 if(++q == sz(G[s])) q = 0; 85 if(now == flow) break; 86 } 87 while(p != q); 88 if(now == 0){ 89 if(--Now[Dfn[s]] == 0) 90 Dfn[src] = n; 91 ++Now[Dfn[s] = tab+1]; 92 } 93 return now; 94 } 95 int getAns() { 96 int flow = 0; 97 memset(Dfn, 0, sizeof Dfn); 98 memset(Now, 0, sizeof Now); 99 memset(Cur, 0, sizeof Cur); 100 Now[0] = n; 101 while(Dfn[src] < n) flow += ISAP(src, inf); 102 return flow; 103 } 104 } solver; 105 106 int idx(char x, int y) { 107 return x*m+y; 108 } 109 bool cango(int x, int y) { 110 return x >= 0 && x < n && y >= 0 && y < m; 111 } 112 int dx[] = {0, 0, -1, 1}; 113 int dy[] = {-1, 1, 0, 0}; 114 115 void calDist() { 116 memset(g, 0x0f, sizeof g); 117 for(int i = 0; i < n*m; i++) g[i][i] = 0; 118 for(int x = 0; x < n; x++) 119 for(int y = 0; y < m; y++) { 120 if(maze[x][y] != ‘.‘) continue; 121 int u = idx(x, y); 122 for(int k = 0; k < 4; k++) { 123 int nx = x+dx[k]; 124 int ny = y+dy[k]; 125 if(!cango(nx, ny) || maze[nx][ny] == ‘#‘) continue; 126 int v = idx(nx, ny); 127 g[u][v] = 1; 128 } 129 } 130 for(int k = 0; k < n*m; k++) 131 for(int i = 0; i < n*m; i++) 132 for(int j = 0; j < n*m; j++) { 133 if(g[i][k] == inf|| g[k][j] == inf) 134 continue; 135 g[i][j] = min(g[i][j], g[i][k] + g[k][j]); 136 } 137 } 138 bool check(LL mid) { 139 src = 2*N+2*n*m; 140 sink = src + 1; 141 solver.init(sink+1); 142 for(int j = 0; j < n; j++) for(int k = 0; k < m; k++) { 143 if(maze[j][k] == ‘#‘) continue; 144 145 int v = idx(j, k); 146 int id1 = 2*N+v*2; 147 int id2 = id1 + 1; 148 solver.add(id1, id2, 1); 149 } 150 // bug(1) 151 for(int i = 0; i < N; i++) { 152 int x = males[i].r, y = males[i].c, t = males[i].t; 153 int u = idx(x, y); 154 155 solver.add(src, i, 1); 156 for(int j = 0; j < n; j++) for(int k = 0; k < m; k++) { 157 if(maze[j][k] == ‘#‘) continue; 158 int v = idx(j, k); 159 // if(u == v) continue; 160 int id1 = 2*N+v*2; 161 int id2 = id1 + 1; 162 // cout << id1 << id2 << endl; 163 // cout << u << v << endl; 164 if(g[u][v] != inf && 1.0*g[u][v]*t <= mid) 165 solver.add(i, id1, 1); 166 } 167 x = fmales[i].r, y = fmales[i].c, t = fmales[i].t; 168 u = idx(x, y); 169 solver.add(i+N, sink, 1); 170 for(int j = 0; j < n; j++) for(int k = 0; k < m; k++) { 171 if(maze[j][k] == ‘#‘) continue; 172 int v = idx(j, k); 173 int id1 = 2*N+v*2; 174 int id2 = id1 + 1; 175 if(g[u][v] != inf && 1.0*g[u][v]*t <= mid) 176 solver.add(id2, i+N, 1); 177 } 178 } 179 // bug(1) 180 return solver.getAns() == N; 181 } 182 int main() { 183 // in 184 185 cin >> n >> m >> N >> M; 186 187 for(int i = 0; i < n; i++) scanf("%s", maze[i]); 188 int ok = 1; 189 int r, c, t; 190 scanf("%d%d%d", &r, &c, &t); 191 r--, c--; 192 if(N-M == 1) { 193 fmales.pb(Node(r, c, t)); 194 } else if(M-N == 1) { 195 males.pb(Node(r, c, t)); 196 } else { 197 ok = 0; 198 } 199 for(int i = 0; i < N; i++) { 200 scanf("%d%d%d", &r, &c, &t); 201 r--, c--; 202 males.pb(Node(r, c, t)); 203 } 204 for(int i = 0; i < M; i++) { 205 int r, c, t; 206 scanf("%d%d%d", &r, &c, &t); 207 r--, c--; 208 fmales.pb(Node(r, c, t)); 209 } 210 211 if(!ok) { 212 puts("-1"); 213 return 0; 214 } 215 N = max(N, M); 216 calDist(); 217 LL L = 0, R = (LL)1e15; 218 // cout << check(R) << endl; 219 //bug(1) 220 while(R-L > 0){ 221 LL mid = (L+R)>>1; 222 223 if(check(mid)) R = mid; 224 else L = mid+1; 225 } 226 if(R != (LL)1e15) { 227 printf("%lld\n", R); 228 } else puts("-1"); 229 return 0; 230 }
G1, G2, G3 Inversions problem
题意：给定长度为n的排列，及k，表示每次可以选取一个区间[li, ri]将其中的数位置反转，求进行k次后逆序对的个数的期望值。
分析：
G1 由于n <= 6, k <= 4, 所以可以直接dp，dp[perm][m]表示排列为perm时，进行m次操作后逆序对的期望值，或者直接模拟每次操作也行。
代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 using namespace std; 16 typedef long long LL; 17 typedef unsigned US; 18 typedef pair<int, int> PII; 19 typedef map<PII, int> MPS; 20 typedef MPS::iterator IT; 21 const int maxn = 110; 22 23 int a[maxn]; 24 int l[maxn], r[maxn]; 25 double ans; 26 int n, k, cnt; 27 28 int getInv(int *a) { 29 int res = 0; 30 for(int i = 1; i <= n; i++) for(int j = i+1; j <= n; j++) 31 if(a[i] > a[j]) res++; 32 return res; 33 } 34 void rev(int *src, int *tar, int l, int r) { 35 for(int i = 1; i <= n; i++) tar[i] = src[i]; 36 reverse(tar+l, tar+r+1); 37 } 38 void dfs(int y, int *src) { 39 int tar[maxn]; 40 if(y == k) { 41 for(int i = 1; i <= n; i++) tar[i] = src[i]; 42 ans += getInv(tar); 43 return; 44 } 45 for(int i = 0; i < cnt; i++) { 46 rev(src, tar, l[i], r[i]); 47 dfs(y+1, tar); 48 } 49 } 50 int main() { 51 // in 52 cin >> n >> k; 53 for(int i = 1; i <= n; i++) 54 scanf("%d", a+i); 55 56 for(int i = 1; i <= n; i++) 57 for(int j = i; j <= n; j++) 58 l[cnt] = i, r[cnt++] = j; 59 dfs(0, a); 60 for(int i = 0; i < k; i++) 61 ans /= cnt; 62 printf("%.12f\n", ans); 63 return 0; 64 }
G2 n <= 30, k <= 200, 数据增大之后肯定不能计算最终排列中逆序对的个数，然后求期望。
可以考虑原排列中x, y dp[x][y][k]表示进行k次操作之后，x, y在原数组中的元素依然能保持原顺序的概率。
这样选取区间[l, r]，转移时4种情况，
1) 区间不反转x 或 y --------- y < l || x > r || (x < l && y > r)
2) 区间仅覆盖x----------------l <= x && x <= r && y >r
3) 区间仅覆盖y----------------l <= y && y <= r && x < l
4) 区间覆盖x和y---------------l <= x && x < y && y <= r
复杂度O(n^4*k)
代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 #define INF 0x0f0f0f0f0f0f0f0f 16 using namespace std; 17 typedef long long LL; 18 typedef unsigned US; 19 typedef pair<int, int> PII; 20 typedef map<PII, int> MPS; 21 typedef MPS::iterator IT; 22 23 const int maxn = 100 + 10; 24 const int maxm = 2000; 25 double dp[maxn][maxn][maxm]; 26 27 int a[maxn]; 28 int n; 29 30 31 int main() { 32 // in 33 int m; 34 scanf("%d%d", &n, &m); 35 for(int i = 1; i <= n; i++) { 36 scanf("%d", a+i); 37 } 38 double ans = 0.0; 39 for(int i = 0; i < maxn; i++) for(int j = 0; j < maxn; j++) 40 dp[i][j][0] = 1; 41 for(int k = 1; k <= m; k++) 42 for(int x = 1; x <= n; x++) for(int y = x+1; y <= n; y++) { 43 double &res = dp[x][y][k]; 44 for(int l = 1; l <= n; l++) for(int r = l; r <= n; r++) 45 if((l > y) || (l > x && r < y) || r < x) 46 res += dp[x][y][k-1]; 47 else if(l <= x && x <= r && y > r) 48 res += dp[r+l-x][y][k-1]; 49 else if(l <= y && y <= r && x < l) 50 res += dp[x][r+l-y][k-1]; 51 else if(l <= x && y <= r) res += 1-dp[r+l-y][r+l-x][k-1]; 52 res *= 2.0/(n+1)/n; 53 } 54 for(int i = 1; i <= n; i++) for(int j = i+1; j <= n; j++) 55 if(a[i] > a[j]) ans += dp[i][j][m]; 56 else ans += 1-dp[i][j][m]; 57 printf("%.12f\n", ans); 58 return 0; 59 }
G3 <= 200，k <= (int)1e9, G3的做法是在上面进行改进的，主要是针对转移部分，计算出转移到dp[x‘][y‘][k-1]的数目。复杂度O(n^3*k)
因为结果会收敛趋于稳定，所以k可取min(k, 1000)，但是
改进后代码还是TLE on test 38。估计优化还不够， 对比他人的代码，冗余运算太多。
上一下代码：
1 #include <bits/stdc++.h> 2 #define pb push_back 3 #define mp make_pair 4 #define esp 1e-14 5 #define lson l, m, rt<<1 6 #define rson m+1, r, rt<<1|1 7 #define sz(x) ((int)((x).size())) 8 #define pf(x) ((x)*(x)) 9 #define pb push_back 10 #define pi acos(-1.0) 11 #define in freopen("solve_in.txt", "r", stdin); 12 #define bug(x) printf("Line : %u >>>>>>\n", (x)); 13 #define TL cerr << "Time elapsed: " << (double)clock() / CLOCKS_PER_SEC * 1000 << " ms" << endl; 14 #define inf 0x0f0f0f0f 15 #define INF 0x0f0f0f0f0f0f0f0f 16 using namespace std; 17 typedef long long LL; 18 typedef unsigned US; 19 typedef pair<int, int> PII; 20 typedef map<PII, int> MPS; 21 typedef MPS::iterator IT; 22 23 const int maxn = 100 + 10; 24 const int maxm = 2000; 25 double dp[maxn][maxn][maxm]; 26 27 int a[maxn]; 28 int n; 29 30 31 int main() { 32 33 int m; 34 scanf("%d%d", &n, &m); 35 m = min(m, 1000); 36 for(int i = 1; i <= n; i++) { 37 scanf("%d", a+i); 38 } 39 double ans = 0.0; 40 for(int i = 0; i < maxn; i++) for(int j = 0; j < maxn; j++) 41 dp[i][j][0] = 1; 42 for(int k = 1; k <= m; k++) 43 // int k = 1; 44 for(int x = 1; x <= n; x++) for(int y = x+1; y <= n; y++) 45 { 46 double &res = dp[x][y][k]; 47 48 //completely not cover [x, y], 49 res += dp[x][y][k-1]*((n-y)*(n-y+1)/2+(x-1)*x/2+(y-x-1)*(y-x)/2); 50 // cout << ((n-y)*(n-y+1)/2+(x-1)*x/2+(y-x-1)*(y-x)/2) << endl; 51 // cout << res << endl; 52 //cover x, not cover y, 53 for(int l = 1; l < y; l++) { 54 if((l<<1)-x > 0 && (l<<1)-x < y) { 55 int cnt = min(y-(l<<1)+x, y-x); 56 cnt = min(cnt, min((l<<1)-x, x)); 57 assert(cnt >= 0); 58 res += dp[(l<<1)-x][y][k-1]*cnt; 59 } 60 61 if((l<<1|1)-x > 0 && (l<<1|1)-x < y) { 62 int cnt = min(y-(l<<1|1)+x, y-x); 63 cnt = min(cnt, min((l<<1|1)-x, x)); 64 assert(cnt >= 0); 65 res += dp[(l<<1|1)-x][y][k-1]*cnt; 66 } 67 68 } 69 //cover y, not cover x, 70 for(int l = x+1; l <= n; l++) { 71 if((l<<1)-y > x && (l<<1)-y <= n) { 72 int cnt = min(n+1-(l<<1)+y, n+1-y); 73 // cout << cnt << endl; 74 cnt = min(cnt, min((l<<1)-y-x, y-x)); 75 assert(cnt >= 0); 76 // bug(1) 77 res += dp[x][(l<<1)-y][k-1]*cnt; 78 } 79 // cout << res << endl; 80 if((l<<1|1)-y > x && (l<<1|1)-y <= n) { 81 int cnt = min(n+1-(l<<1|1)+y, n+1-y); 82 cnt = min(cnt, min((l<<1|1)-y-x, y-x)); 83 assert(cnt >= 0); 84 res += dp[x][(l<<1|1)-y][k-1]*cnt; 85 } 86 // cout << res << endl; 87 } 88 // cout << res << endl; 89 //cover [x, y]. 90 for(int l = 1; l <= n; l++) { 91 if((l<<1)-x > 0 && (l<<1)-x <= n 92 &&(l<<1)-y > 0 && (l<<1)-y <= n) { 93 94 int cnt = min(n+1-(l<<1)+y, n+1-y); 95 cnt = min(cnt, min((l<<1)-y, y)); 96 cnt = min(cnt, min(n+1-(l<<1)+x, n+1-x)); 97 cnt = min(cnt, min((l<<1)-x, x)); 98 assert(cnt >= 0); 99 // cout << cnt << endl; 100 res += (1-dp[(l<<1)-y][(l<<1)-x][k-1])*cnt; 101 } 102 if((l<<1|1)-x > 0 && (l<<1|1)-x <= n 103 &&(l<<1|1)-y > 0 && (l<<1|1)-y <= n) { 104 int cnt = min(n+1-(l<<1|1)+y, n+1-y); 105 cnt = min(cnt, min((l<<1|1)-y, y)); 106 cnt = min(cnt, min(n+1-(l<<1|1)+x, n+1-x)); 107 cnt = min(cnt, min((l<<1|1)-x, x)); 108 assert(cnt >= 0); 109 res += (1-dp[(l<<1|1)-y][(l<<1|1)-x][k-1])*cnt; 110 } 111 } 112 res *= 2.0/(n+1)/n; 113 } 114 for(int i = 1; i <= n; i++) for(int j = i+1; j <= n; j++) 115 if(a[i] > a[j]) ans += dp[i][j][m]; 116 else ans += 1-dp[i][j][m]; 117 printf("%.12f\n", ans); 118 return 0; 119 }
原文：http://www.cnblogs.com/rootial/p/4289327.html
