3.1. 如是我闻
“是闻”的意思是“听说是酱紫的”,“如是我闻”的意思就是“就像我听说的那样”。大部分佛经都是以“如是我闻”开头,意思是“就像我听佛陀说的那样”。硕士期间,浪费了一大部分时间整天沉浸在“如是我闻”的句子里。话说回来,“如是我闻”是鸠摩罗什第一个翻译的,人不但佛学得好,而且还是“译神”(翻译之神)。严复提出了后世膜拜不休的翻译准则:信、达、雅。而他也正是从鸠摩罗什的译经中学来的。所以读佛经,就好像是在读一篇遣词造句超然天工的美文,更重要的是里头的禅意甚深。以至于,后来很多湿人在满级之后,都开始写禅偈子,然后很风骚地给自己加一个“居士”的称号。大家可以翻翻中小学课本,看看有多少湿人都有一个“什么什么居士”的头衔。对,没错!他们不是真的信佛,他们是在装。
其实很多佛经都是后世人按自己的体悟,大开脑洞后写的,然后在最前面加一句“如是我闻”——“我是听佛陀说的”。这就叫,装完之后再谦虚一下。
所以,我要表达的是,我接下来讲的这些真的不是在装,真的是听别人说,或者看到别人这样写的,而我又觉得可以跟大家分享分享。
3.2. 再谈同构
很多人开脑洞,谈佛学和量子力学的共通性,大家感兴趣可以网上搜搜。很多讲的很好的人都是对佛学不了解,对量子力学也不了解的那些人。讲得好就是要把明白的人讲晕,把不明白的人讲的更晕,然后,they did it!
其中一个吹得还有那么点意思的是曹天元的《上帝掷骰子吗》,之前M同学推荐给我,我也找过来拜了一拜。里面很风趣地讨论了唯物派对人类意识的一些观点,其中就包括同构。说人类特有的意识仅仅是取决于某种“组合模式”,而不限定于特定的物质。然后M同学举了个很有意思的例子:把大萝卜们按照人类大脑的结构进行组合,那么这些萝卜就可以开始思考:“我为什么是萝卜?”这个问题了。我觉得这个例子很有意思,就放在了这里。下面再展开谈谈2.5提到的“同构”。
这些在谈“归约”之前谈,我觉得或多或少对大家有点帮助。同构说的是,两个不同的事物之间存在着高度的相似性,在谈计算复杂性的背景下,就是两个计算问题之间存在着高度的相似性。然后利用这种相似性,我们将一个问题A“规约”到另一个完全不一样的问题B上去,那么解决A就可以通过解决B来完成。
也许现在你还没有什么感觉,但是再仔细感受感受,两个风马牛不相及的问题竟然是相似的,这本身不是一件很有意思的事情吗?就像《GEB》的作者开脑洞后发现,逻辑、绘画、音乐之间竟然也存在惊人的相似性。你难道不觉得“大自然暗示我们两个完全不一样的东西背后竟然是如此地一致”这件事儿是故意安排的吗?
从计算机角度看来,这个稍微容易理解一点。两个同构的问题,比如SAT和Circuit(就不在这里介绍什么是SAT和Circuit问题,不影响阅读),它们最后都被编码成了01串,说白了解决这两个问题就是在对这些01串进行操作。对SAT的01串的一个操作,我们用一系列对Circuit的01串的操作来模拟,反之亦然,由此产生同构。
在计算机里,虽然两个问题可以互操作(比如上面讲到的SAT和Circuit),但是它们还是两个不同的问题,只是背后存在着相似性。互操作,只是因为它们在计算机中都被编码成了01串,然后我们都是对01串进行操作。我再举个例子,W老师上课给出了一个语言,名叫L语言,它只能进行下面三种操作:
X <- X+1 X <- X-1 IF X GOTO [A] |
如上面表中所示,L语言只能进行累加、递减和条件转移操作,但是L语言已经被证明是图灵完备的,也就是它可以模拟任何复杂的语言。如果有一台机器是根据L语言造出来的,那么用这台机器来解决问题时,所有的问题到最后都是这三条指令的操作序列。而同构的两个问题A和B之间,就可以通过限定指令的操作方式来相互模拟了:即对A的一个操作,可以用对B的一系列操作来实现,反之同理。
回到现实世界,完全不一样的东西背后存在惊人的相似性。那么这种相似性本身是怎么来的呢?它们可以通过互操作相互模拟吗?很遗憾,现在还没有人有任何实质性的实验结论。不过小学时语文老师可能会教你一个邪招:通感。比如在文章里插一句“这个美丽动听的声音听上去真的是五颜六色啊”,然后作文肯定可以很顺利地拿到不及格。
3.3. 把一个判定问题看成一种“语言”
上面提到的两个同构问题A和B可以相互模拟,你如果觉得不能理解,我用另外一种表达方法:A可以用B来描述。然后你会说,“不好意思,我更不懂了。”
很多教科书抄别人的说法,在谈归约的章节里,把一个判定问题直接用一种语言(比如:L)来表达,也根本不讲清楚来龙去脉。OK,如果你已经把这本教科书放到了厕纸筒里,那请你今天就把这几章用掉。
首先放三个问题:1)为什么要把一个判定问题看成是一种语言? 2)什么是“语言”? 3)怎么把一个判定问题看成一种语言?
为什么天朝的大部分教材很bull shit呢(注意限定词是大部分,不是全部)?因为它们从来都不会去讲“为什么”;而为什么洋人的教材个个都长得都跟脑白金超值礼品套装盒一样,因为他们苦口婆心反反复复就跟你在叨咕这个“为什么”。我们的教育为什么bull shit?因为我们从来都不会引导孩子去思考“为什么”,导致我们长大后有一种惯性思维便是:“是这样就成,咋来的无所谓”。我家楼上原来住着一个做钢筋混凝土发了财的壕叔,有钱后娶了一个棒子媳妇儿。我老娘管事儿,问他:“干嘛娶个韩国媳妇儿?”他想了想说:“就是那个漂亮啊!”直到娃出来之后,他才发现:呀,媳妇儿是经过后期处理的啊!
回到正题,我们先来回答第一个问题:为什么要把一个判定问题看成是一种语言?对于这类的问题,一般只有一个原因就是:省事儿!就跟人们谈P=?NP问题时只关注判定问题一样。从语言的角度来谈同构,或者后面要讲的归约,事儿就方便了。但是,把问题看成一种语言也好,关系也好,函数也罢,其实都一样。从多个角度来描述或者解释一个对象,往往会有惊讶的发现(这些发现往往也都是你感受到了某种“同构”的存在)。也有人不喜欢这么做,比如有一个处女座的科学家,喜欢用函数来描述问题,于是谈可计算性和计算复杂性的时候从头到尾全是用的函数。虽然这是一本经典,不过搂了一眼后你还是会感叹,处女座真可怕!
第二个问题:什么是语言?这个问题太大,就算是搞语言学的人都无法给个完全的定义。我们既然是研究计算机的问题,那更多地是从数学的角度出发。对于这个问题,我们只要找到一种可以对语言建模的数学模型就可以了。一个最简单的模型就是集合。我们假设用集合L来代表一种语言,并且规定L中的元素是在某种约束下的所有合法的句子,形式化如下:
定义7:L是一种语言,且 L={X?Σ*|P(X)},其中,Σ是字符表,接收函数P(X)是一个布尔函数,用于判定X是否可以被该语言接收。
在上面这个定义中,语言是一个集合,并且是合法的句子(更确切地,应该是字符串,不引起歧义的情况下我们在这里以及后文就用“句子”来表达合法的字符串)的集合,你不用去纠结集合里的是词素,句子,短语还是篇章,只要这个字符串X被P(.)这个布尔函数判定为true(“接收”)就成。P(.)对于一个语言系统来讲起到了约束,限定的作用,或者更确切地说是语法或者文法。如果把一个语言的诸多约束或者语法看成是一个个函数,那么P(.)可以看成是这些函数的复合。举个栗子:
语言1:L1 ={X?{0,1}*|isPalindrome(X)}.
语言L1的接收函数是isPalindrome,用于判定输入的串是否是回文,而L1中的所有句子都限定在01串的范围内,所以L1语言实际上是所有的01回文串组成的集合。
但实际生活中的语言(或者称之为自然语言),它们的语法系统肯定是在不断地更新中,所以语言所对应的集合也一定在不断地扩充或者缩减。更普遍地,两种语言系统也会融合。比如,上次问俩哥们儿,周末准备去哪儿玩儿,他们说准备去XX家里玩“轰趴”。我说,纳尼,你们原来是这个倾向?!后来才了解到是我自己奥特了,“轰趴”就是家庭聚会的意思。但是假如他们说,我们准备去XX家里进行一次家庭聚会。嗯,这就感觉,到时去XX家时会全体起立,奏国歌一样。语言的改变更多地发生在年轻人的群体当中,灵活,亲切,而所有的目的就是为了:方便。
有了上述对语言的简单定义,那么第三个问题就水到渠成。因为判定问题在第一篇笔记当中也已经用集合来定义,所以ofcourse可以把一个判定问题看成是一种语言。很多教科书直接很酷炫地拉出来,“我们现在把一个判定问题编码成一种语言”。实际上真正要到这一步,我们要经过上面这么多理解之后才行。我们把一个判定问题R看成一个语言LR,那么首先要注意的是,这个LR其实是判定问题R的所有被特征函数判定为“true”的输入的集合。此外,要把R和LR对应上,最重要的是要把R的特征函数看成是LR的接收函数。另外,由于判定问题的特征函数是固定的,问题域也是相对不变的,所以我们这里所研究的这些个语言基本上都是静态的。
我们以问题4,判断x是不是质数?来说明。这个判定问题形式化为R={x?N|Prime(x)}。它本身也是一种语言L2:
语言2:L2 ={X?N|Prime(X)}.
它的合法的句子就是所有质数(当然可以编码成0,1串的形式,或者直接以阿拉伯数字的形式出现),而它的接收函数也就是Prime(x)。是不是so easy?
现在,我们回到这一节的开头,如何用一个问题A来描述另一个问题B?前面我们说过,任何问题都对应一个判定问题。所以我们关注更具体的一个问题:如何用一个判定问题A来描述另一个判定问题B?那到此为止,我们知道A和B都对应一个语言,假设为LA和LB,所以我们要考察如何用语言LA来描述LB。
什么叫用一种语言来描述另一种语言?很简单,对应到我们的自然语言,就是“翻译”。当然,我们不需要做到鸠摩罗什的信、达、雅,对于“Oh,My GOD!”,你of course 可以翻译成“我勒个去!”用LA来描述LB,就是把LB翻译成LA,所以最后翻译出来的那个东西LC实际上是LA的一个子集,但是同时能描述LB的性质。换句话说,LC和LB是同构的,但,是LA的子集。
上栗子,我们用语言1试着来描述语言2。
怎么在语言1中找一个子集,而这个子集又能描述语言2的性质呢?首先,语言2中都是自然数,而语言1中只是01串,所以不能直接将语言2作为语言1的子集。
那么把语言2的元素都用二进制形式表示?当然也不可以,对于最小的质数2,其二进制形式是01,却不是一个回文。
也许你会问,语言1只是01回文串的集合,它的表达能力可能根本就不足以描述出语言2啊?
现在就需要你开脑洞了。想一想,这里判定问题所对应的语言不像我们日常生活中的语言系统那么复杂,它们中的句子往往仅具有一种非常简单的“共有”性质。对于语言2,所有的句子都是质数,而Prime(.)就是它们唯一的共有性质,也就是说只要这个语言能表达出(或者界定出)质数就可以了。而现在,我们只要从语言1里找一个子集,这个子集的元素在某一方面也具有“质数”这个共有性质。我于是找到下面这个语言:
语言3:L3 ={X?0*|Prime(length(X))? isPalindrome(X)}.
L3中句子的字符都是“0”,所以肯定符合回文形式,而我将L3进一步限定在串长是质数的范围内。因此,L3即是L1的一个子集,而其元素的长度又能表达出质数这个性质。所以,L3可以作为语言1对语言2的描述。
你也许要反驳了,我的做法是犯规的,突然加上“串的长度”是不是作弊?这并没有作弊,因为L3仍旧是L1语言(或者说子集)。我所做的是在L1语言的语法层多加了一种属性“串的长度”来进一步限制了一下,但本身并没有逾越L1语言的范畴。如果,外星人来访问,而它们只用一进制,那我们也只能用L3来描述质数了不是嘛。
什么叫逾越L1语言的范畴?按照定义7,一种语言实际上分成两个层次,一个就是语言层:包含所有的合法句子;另一个是语法层:是来限定或者描述这个语言的特性、范围。从数学系统的角度来讲,语法层更像是一种元语言,这种元语言定义出了更具体的语言。具体来说,如isPalindrome(.)这个接受函数本身也是一种语言(布尔函数),不妨称之为MetaL1,用它来定义出了更具体的语言L1。如果,L1越庖代俎要试图去描述MetaL1,OK,这时就已经逾越了L1本身的范畴了。更通俗地讲,上帝创造了我们人类,而我们人类又反过来质问:上帝本身是不是我们创造的?这事儿严重了,上帝要生气了。我们到下一节来简单谈谈这个问题:自指。
3.4.自指
从哲学的角度来看,让人类产生烦恼的根本原因是人类意识到了“自己究竟是什么玩意儿?”这个很严重的问题。不过我们这个笔记不会试图去回答这个问题。只是这个现象本身和我们接下来要聊的东西很像:自指。
自指没有一个明确的定义,因为这个现象在哲学,语言,数学,逻辑学甚至经济学(阿罗悖论)里都存在。我们接着3.3的茬,对于语言L1,它的语法(或者接收函数)本身需要一种语言MetaL1来描述和表达(不妨称之为描述语法的元语言),如果L1中的句子试图去描述MetaL1的话,那么就产生了自指。我们说这些句子越庖代俎了,做了老子该做的事儿。不做自己本分的事儿,并且还做不好那就要出问题。我们在笔记二里举了个例子,这里简化一下来说明我们日常生活的语言中出现的自指现象:
问题6:下面这句话是错的吗?
我这句话是错的。
假设我们世界里的话们(句子们)只有对错之分,也就是所有的话有一个“对”或者“错”的属性。那么哪一句话是对,哪一句话是错,这个就是语言的规则系统或者语法系统规定的事儿。现在,“我这句话是错的”本身是这个世界里的一句话,但是它试图代替语法系统来定义自己的对错。如果语法规定“我这句话是错的”是错的话,那么根据这句话本身的描述又应该是对的;如果是对的,那么“我这句话是错的”就没有错,那么应该是错的。现在,就粗事儿了,到底是对是错?这个例子是对说谎者悖论的另一种表达。
我们之前定义语言的时候,把语言看成一个集合。如果仅仅从集合这个数学系统来解释自指,就是说集合中的元素试图去描述这个集合本身。假设有一个集合S={X|X?X},S是这样一类元素的集合,这些元素不属于它们自身,那么S是不是属于S自己呢(S??S)?如果S属于自己,那么它就不符合“X?X”这个特征函数;如果不属于自己,那它应该在自己中,又和“不属于自己”矛盾了。罗素发现的这个悖论用很简单的方式说明了数学系统并不完善。后来大家伙儿开脑洞,开出了一个更通俗的例子:理发师悖论。构建一个完美的数学系统的梦最终被哥德尔打破,我们这里挂上艾舍尔的一副经典作品《绘画的手》以示对各种大师们的敬仰:
解决由自指导致的问题,很简单的方法就是加上“禁止你做老子该做的事儿”之类的限制。比如问题6,既然“对”和“错”是语法层赋予句子的属性,那么具体的每一个句子中就不应该再出现对自身或者其它句子的“对”或者“错”的描述。在数学系统当中也可以引入类似的限制,比如类型论所做的事情(它也号称解决了第二次数学危机)。不过这些做法到头来像是仅获得了一些心理上的安慰,而并不能掩盖一个事实:我们这个世界并不那么完美。
3.5 停机问题
由自指引发的矛盾,通常可以用来证明。在可计算性理论中,最基本的不可计算问题——停机问题,它的不可计算性就可以通过自指来证明。下面我们就以停机问题为例来看看自指怎么用来证明。
在给出停机问题的定义和其不可计算性的证明前,我们先来介绍一个编码函数:哥德尔编码:
G?del([X1,X2,…Xi,…,Xn]) =
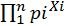
给定一个有序的自然数列[X1,X2,…,Xn],其中X1到Xn是n个任意的自然数。哥德尔编码函数G?del()就是以任意的自然数列作为输入,然后是一个累积连乘式,每一项是一个指数形式,以第i项为例: ,幂就是输入的数列中第i个数Xi,底数是第i个质数Pi(比如第三个质数是P3= 5)。G?del编码可以将不同的数列对应到唯一的一个自然数。这个从另一方面也说明了自然数是无穷的。
,幂就是输入的数列中第i个数Xi,底数是第i个质数Pi(比如第三个质数是P3= 5)。G?del编码可以将不同的数列对应到唯一的一个自然数。这个从另一方面也说明了自然数是无穷的。
有了哥德尔编码,我们就可以将一个程序P编码成一个唯一的自然数#P。假设程序是由一条条指令组成的,在32位机也好64位机也好,每一条指令假设都对应了一条二进制编码。如果我们将每一条指令的二进制编码转译成一个自然数,那么每一条指令都对应唯一的一个自然数(不同的指令之间一定存在某一位不一样)。而每一个自然数也可以通过求取其二进制形式翻译出这条指令。通过这种方式,程序P就可以看成是一个自然数列,第i项就对应了其第i条指令,那么也就存在唯一的一个自然数与P对应,即
#P =G?del(P)
从某个自然数解码出这段程序也就很显然了:
P =de-G?del(#P)
这里de-G?del()是G?del的反函数。对于某一台的机器,每一个自然数都会对应唯一的一段程序。不同的机器之间可能某一个自然数对应的程序不一样,这取决于机器的指令系统。
在哥德尔编码的基础之上,我们就可以定义出停机问题:
定义7(停机问题):给定一个程序P,和谓词Halt(#P, X)。在P输入为X的情况下,如果P停机, Halt(#P,X) = true,否则Halt(#P, X) = false。
这里假设程序P的输入只有一个自然数X。当然,程序可能有多个输入参数,如果按照这些参数的输入顺序求取G?del编码,那么也可以用唯一对应的一个自然数来作为输入。
接下来我们证明停机问题不可计算。首先,什么叫可计算,什么叫不可计算?在可计算性理论中,所谓一个问题可计算,就是将它交给计算机来处理时,存在一个程序能够把这个问题解出来。所以就算一个问题本身是有解的,或者有答案的,计算机也不一定能够解出来。就像停机问题,从定义来看,对于一段程序肯定要么停机要么不停机,所以Halt()函数肯定有解(或者肯定是全函数),但是定理3表明计算机本身解决不了这个问题。
定理3:停机问题不可计算。
证明,
利用反证法,假设停机问题可计算,然后推出矛盾。对于某一段程序P,我令它的输入是它自身的哥德尔编码,即X=#P,那么按照假设我们就有Halt(X,X)是可计算的(也就是程序一定会返回Halt(X,X)是true还是false)。现在我们构造另一个程序P’:
while(Halt(X,X)); |
P’输入仍旧是X,只是它调用了P来做while循环的条件判断,如果Halt(X,X)为true,那么就永远不会跳出while循环。令Y=#P’,那么Halt(Y,X)=false。也就是
Halt(Y,X)=~Halt(X,X)
因为P并没有指明是什么具体的程序,所以我令P这个程序就是P’。所以也有下面的结论:
Halt(Y,Y)=~Halt(Y,Y)
这显然是个矛盾。证毕。
这个证明简单点说,就是一个不停机的程序试图判断自己停不停机。证明巧妙地利用了自指。后来很多不可计算问题都是基于停机问题不可解来证明的。大一的小盆友们刚上C语言课时,老师会介绍算法和程序的区别,而这区别也就是算法要求停机。以前有个学金融的友人准备考计算机二级证,问我为什么算法要求停机,我一下子觉得自己过去的人生受到了质疑,因为我从来没想过这个问题!现在终于想明白了,因为算法就是要去解决问题的嘛。
当然,自指还可以用于证明其他问题,比如数理逻辑中,经常定义出一种叫canonical解释的模型来证明完备性啥的。对于自指的这些具体应用,这个笔记里就不细说了。
3.3. 接下来
先回顾一下到目前为止我们做了些什么,后面又要去做些什么,然后再继续上路。
我们要研究计算问题的复杂性,这里复杂性要明确的是交给机器来计算、或者用一个程序来运行有多少复杂,而不是人为的。人解决问题是会受环境因素影响的,比如我为什么考上了现在的大学,而没有考取清华?因为高考时坐在后面的一个胖子竟然在哼我最喜欢的Linkin Park?!但是问题交给机器来解决,除非把计算机放在炼丹炉里,否则就一定会有一个自然存在的复杂程度。
那么,接下来,要解决的计算问题是什么呢?我们在第一篇笔记和第二篇笔记的开头将计算问题限定在了一个范围内,我们仅仅在那个范围内进行考察。这里面的计算问题是“实实在在”的计算问题,给定一个输入,计算得到输出。所以,不是证明(the procedure of proof),即,推导出一个已经给定的结论。这些计算问题就像是W老师用来碾压我们的他的四年级女儿的奥数习题。因此,研究计算问题,一定要清楚,我们其实是回到了我们的出发点,去看看那些我们从小就在解决的计算问题到底可以在多好的性能内被自动化地解决。
界定了计算问题之后,我们在之上定义了四类计算问题PC,PF,P,NP。这四类是按照时间复杂性来分的类别。按照计算形式分类,这四类计算问题又属于两个大类:搜索问题和判定问题。但发展到现在,计算复杂类家族中有上百种类别,之所以从多项式时间出发以及给出定义,是因为我们日常生活中大部分问题都是多项式时间内可解的,或者多项式时间内可验证解答的。解决多项式时间的问题确实对我们在很多方面是有帮助的,所以一切从多项式时间开始。
多项式时间内可以解决的问题(P)是已经找到了一个多项式时间的算法,或者证明出来存在这样的算法。然而,多项式时间内可以验证解答的问题(NP)也是非常普遍的一类问题。但问题是,人们到现在还没能够找出或者证明NP类问题是否存在一个多项式时间的算法。即使是“不存在”也难以证明。
我们现在找不到NP问题的多项式时间算法,那么我们先来看看有哪些问题是NP问题,它们之间是否存在关联。如果存在关联,那么当我们找到一个NP问题的多项式时间算法时,是不是也能找到其他问题的多项式算法。于是,我们想到了同构,如果一些问题可以同构或者归约到一个问题,那么解决这个问题就可以解决所有的问题。关于同构,我们讲了很多废话,也竟然延伸到了自指,以至于你也许早就放弃读我的笔记了。
不管怎样,下面回归正途,在接下来的笔记里谈谈多项式归约。
原文:http://my.oschina.net/airship/blog/378824