状态压缩插头DP
HDU 1693 Eat the Trees
http://www.cnblogs.com/zhuangli/archive/2008/09/04/1283753.html
http://blog.csdn.net/xymscau/article/details/6756351
题意:在N*M(1<=N, M<=11)的矩阵中,有些格子有树,没有树的格子不能到达,找一条或多条回路,吃完所有的树,求有多少种方法。
分析:轮廓线表示当前插头的状态,这题中状态中1表示有插头,0表示无插头。如果是横线的话就是上面的格子与下面的格子相连的状态,这题中显然一个格子中要么有两个插头(经过这个格子),要么没有插头(不经过这个格子),因为不可能分叉走,每个格子走一次。
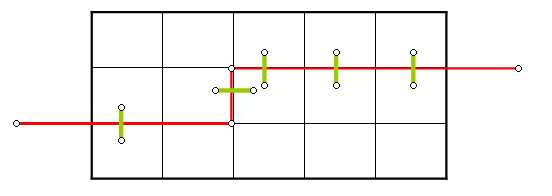
上图状态表示(101111),当前决策格子是第二行第三个格子,显然它已经有了两个插头,也就是有1条线穿过它,所以不用再加插头了。
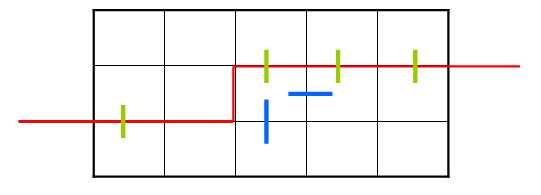
上图状态(100111),当前决策格子是第二行第三个格子,显然有一个下插头了,再添加一个右插头即可,那么就有两个选择,要么向下,要么向右,就要有两个转移。
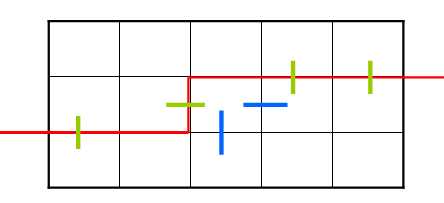
上图状态(101011),当前决策格子是第二行第三个格子,显然有一个右插头了,再添加一个下插头即可,那么就有两个选择,要么向下,要么向右,就要有两个转移。
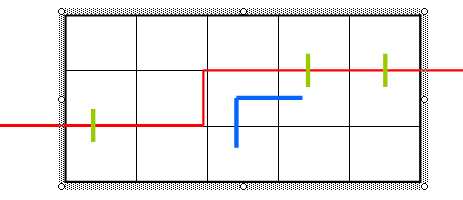
上图状态是(100011),当前决策格子是第二行第三个格子,显然之前没有插头,只能添加两个,或者不添加。不添加,就肯定不经过这个格子,显然只能这个格子是障碍。

#include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<iostream> #include<cmath> using namespace std; int gp[12][12]; __int64 dp[13][13][1<<13]; int n,m; void DP() { memset(dp,0,sizeof(dp)); dp[0][m][0]=1; for(int i=1;i<=n;i++) { for(int j=0;j<(1<<m);j++)//把上行最后列的状态平移到下行第一列之前,即下行0列状态。 dp[i][0][(j<<1)]=dp[i-1][m][j];//因上行在逐格向右推时,会把状态向右移一位,所以要左移1位 for(int k=1;k<=m;k++) { for(int sta=0;sta<(1<<(m+1));sta++) { int y=1<<k; int x=1<<(k-1); if(gp[i][k])//可经过该点 { if((sta&x)!=0&&(sta&y)!=0)//当前状态有下和右插头,只能从没有上和右插头状态转移来 { dp[i][k][sta]=dp[i][k-1][sta-x-y]; } else if((sta&x)==0&&(sta&y)==0)//当前状态无下和右插头,只能从有上和右插头状态转移来 dp[i][k][sta]=dp[i][k-1][sta+x+y]; else//当前状态只有一个插头,则可以从原状态和添加另一个插头转移来。添加另一个插头状态相当于另起一个连通分量。 dp[i][k][sta]=dp[i][k-1][sta^x^y]+dp[i][k-1][sta]; } else//不能经过该格子 { if((sta&x)==0&&(sta&y)==0)//无插头,表示不需要经过此点,直接就转移过来 { dp[i][k][sta]=dp[i][k-1][sta]; } else//有插头,走不动,则只能是0种方式。 dp[i][k][sta]=0; } } } } printf("There are %I64d ways to eat the trees.\n",dp[n][m][0]); } int main() { freopen("xx.in","r",stdin); int c,cn=0; scanf("%d",&c); while(c--) { cn++; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { scanf("%d",&gp[i][j]); } } printf("Case %d: ",cn); DP(); } return 0; }
原文:http://www.cnblogs.com/lizw0520/p/4293404.html