题目来源是CSDN:http://club.csdn.net/module/club/student/programming_challenges
一个三角形必然存在它的内切圆与外接圆,求他们的面积比。
考虑到精度问题,我们输出面积比*1000的整数部分(直接下取整)。
输入数据是一个三角形的三个顶点,但这三个顶点在三维空间中,所以输入是9个整数,
分别表示三个顶点(x1,y1,z1) (x2,y2,z2) (x3,y3,z3),保证三点不共线,每个整数在-1000,+1000范围内。
输出内接圆与外切圆的面积比*1000的整数部分。
这个题其实关键是对几何公式的运用:
(1)用三维坐标系中计算两点距离的公式计算三角形的三条边a、b、c。(公式参考百度百科)

(2)计算内切圆半径r。(公式参考维基百科)

下面是对公式的推导:
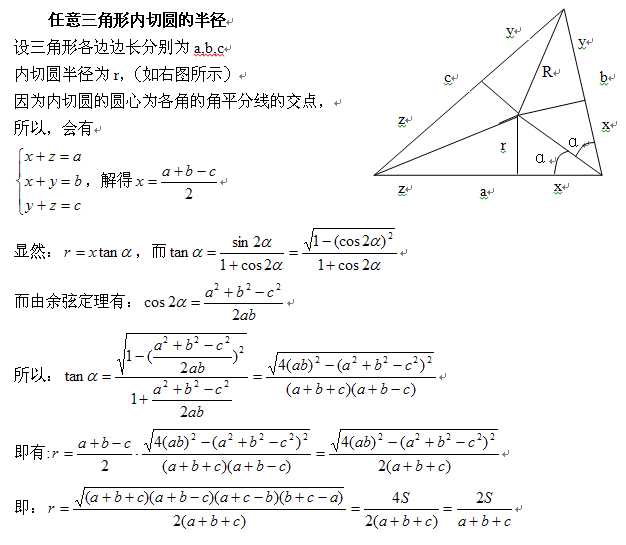
(3)计算外接圆的半径R。
公式参考如下:

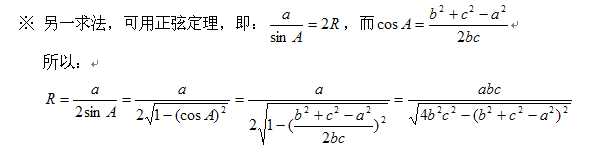
(4)上面计算r、R的过程需要用到三角形的面积S。
根据三角形三边长a、b、c计算面积S可以用海伦公式:(维基百科)

(5)计算出了r、R就可以计算内切圆和外接圆的面积之比了。
这个计算量还是不小的,慢慢算吧。
原文:http://www.cnblogs.com/huashanqingzhu/p/3525049.html