Kind of a Blur

Image blurring occurs when the object being captured is out of the camera‘s focus. The top two figures on the right are an example of an image and its blurred version. Restoring the original image given only the blurred version is one of the most interesting topics in image processing. This process is called deblurring, which will be your task for this problem.
In this problem, all images are in grey-scale (no colours). Images are represented as a 2 dimensional matrix of real numbers, where each cell corresponds to the brightness of the corresponding pixel. Although not mathematically accurate, one way to describe a blurred image is through averaging all the pixels that are within (less than or equal to) a certain Manhattan distance?from each pixel (including the pixel itself ). Here‘s an example of how to calculate the blurring of a 3x3 image with a blurring distance of 1:


Given the blurred version of an image, we are interested in reconstructing the original version assuming that the image was blurred as explained above.

2 2 1
1 1
1 1

3 3 1
19 14 20
12 15 18
13 14 16

4 4 2
14 15 14 15
14 15 14 15
14 15 14 15
14 15 14 15

0 0 0

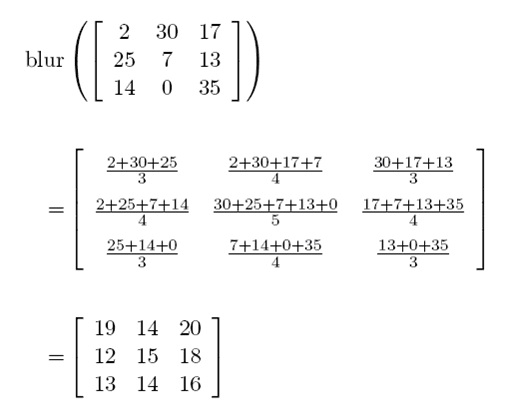
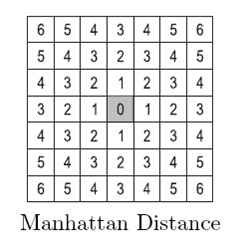
    1.00    1.00
    1.00    1.00

    2.00   30.00   17.00
   25.00    7.00   13.00
   14.00    0.00   35.00

    1.00   27.00    2.00   28.00
   21.00   12.00   17.00    8.00
   21.00   12.00   17.00    8.00
    1.00   27.00    2.00   28.00
Hint
The Manhattan Distance (sometimes called the Taxicab distance) between
two points is the sum of the (absolute) difference of their coordinates. 
The grid on the lower right illustrates the Manhattan distances from the grayed cell.
 

高斯消元法模板题，测试模板。

代码：

#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-8
#define pi acos(-1.0)
typedef long long ll;
double s[20][20],a[200][200],x[200];
int equ,var;
int Guass(){
	int i,j,k,col,max_r;
	for(k=0,col=0;k<equ&&col<var;k++,col++){
		max_r=k;
		for(i=k+1;i<equ;i++)
			if(fabs(a[i][col])>fabs(a[max_r][col]))
				max_r=i;
		if(fabs(a[max_r][col])<eps)return 0;
		if(k!=max_r){
			for(j=col;j<var;j++)
				swap(a[k][j],a[max_r][j]);
			swap(x[k],x[max_r]);
		}
		x[k]/=a[k][col];
		for(j=col+1;j<var;j++)a[k][j]/=a[k][col];
		a[k][col]=1;
		for(i=0;i<equ;i++)
			if(i!=k){
				x[i]-=x[k]*a[i][k];
				for(j=col+1;j<var;j++)
					a[i][j]-=a[k][j]*a[i][col];
				a[i][col]=0;
			}
	}
	return 1;
}
int main()
{
     //freopen("data.in","r",stdin);
     //freopen("data.out","w",stdout);
	 int d,tt=0,m,n;
     while(~scanf("%d%d%d",&m,&n,&d)&&(n+m+d)){
		 if(tt++)puts("");
		 for(int i=0;i<n;i++)
			 for(int j=0;j<m;j++)
				 scanf("%lf",&s[i][j]);
		 memset(a,0,sizeof(a));
		 equ=var=n*m;
		 for(int i=0;i<n;i++)
			 for(int j=0;j<m;j++){
				 int cnt=0;
				 for(int k=0;k<n;k++)
					 for(int p=0;p<m;p++)
						 if(abs(i-k)+abs(j-p)<=d){
							 a[i*m+j][k*m+p]=1;
							 cnt++;
						 }
				 x[i*m+j]=cnt*s[i][j];
			 }
		 Guass();
		// cout<<ha<<endl;
		 for(int i=0;i<n;i++){
			 for(int j=0;j<m;j++) 
				 printf ("%8.2lf", x[i*m+j]);
			 puts("");
		 }
	 }
     return 0;
}

hdu 3359 高斯消元法,布布扣,bubuko.com

hdu 3359 高斯消元法

原文：http://blog.csdn.net/xianxingwuguan1/article/details/20703889