我们先来介绍一下尺取法。尺取法,顾名思义,像尺子一样,一块一块的截取。是不是解释的有点让人纳闷~。。没关系,下面我们通过这个题目来体会尺取法的魅力。
题目翻译:
给定长度为n的数列整数a0,a1,a2,a3 ..... an-1以及整数S。求出综合不小于S的连续子序列的长度的最小值。如果解不存在,则输出0。
限制条件:
10<n<10^5
0<ai<10^4
S<10^8
这里我们拿第一组测试数据举例子,即 n=10, S = 15, a = {5,1,3,5,10,7,4,9,2,8}
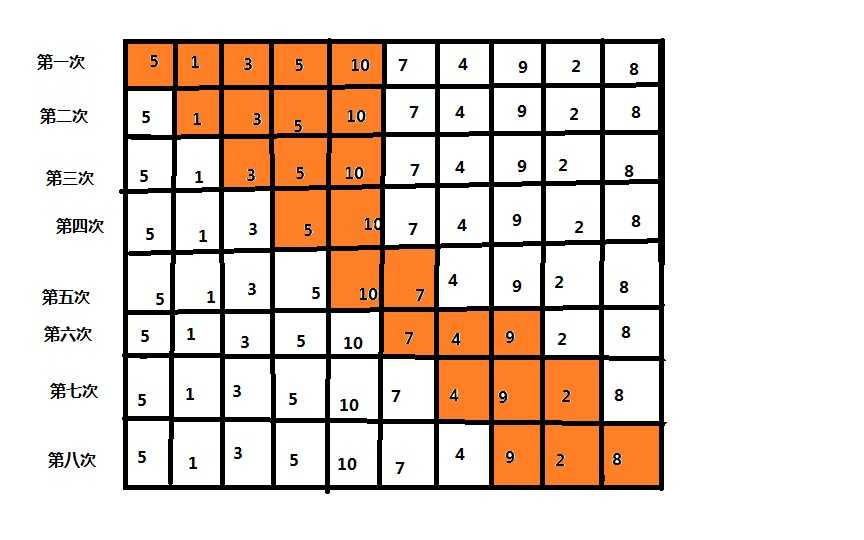
这幅图便是尺取法怎么“取”的过程了。
整个过程分为4布:
1.初始化左右端点
2.不断扩大右端点,直到满足条件
3.如果第二步中无法满足条件,则终止,否则更新结果
4.将左端点扩大1,然后回到第二步
用尺取法来优化,使复杂度降为了O(n)。
最后,再给一个尺取法的定义以便更好理解:返回的推进区间开头和结尾,求满足条件的最小区间的方法称为尺取法。
以上为网上关于尺取法的原理介绍,还是比较好理解的,邢如蚯蚓的爬动。
直接上代码:
-
#include "stdafx.h"
-
#include <set>
-
#include <map>
-
#define MAXN 10
-
#define S 11
-
#define min(x,y) (x>y?y:x)
-
int sequence[MAXN] = {5,1,3,5,10,7,4,9,2,8};
-
-
int slove(int sequence[])
-
{
-
int s = 0, t = MAXN , sum = 0 , i = 0;
-
int res = MAXN + 1;
-
while (1)
-
{
-
while (sum < S && i < MAXN)
-
{
-
sum += sequence[i++];
-
}
-
if (sum < S)
-
{
-
return res;
-
}
-
if (res > MAXN)
-
{
-
printf("not find \n");
-
return res;
-
}
-
res = min(res,(i - s));
-
sum -= sequence[s];
-
s++;
-
}
-
}
-
-
int _tmain(int argc, _TCHAR* argv[])
-
{
-
int res = slove(sequence);
-
printf("res is %d\n",res);
-
return 0;
-
}
今天开始学算法系列 -- 尺取法
原文:http://blog.chinaunix.net/uid-24922718-id-4848418.html
