年前的时候去逛书店,久仰算法导论这本书的大名看见后也就买了下来。回家看了一段时间,发现看书的进度真的是极慢,书里的课后题很多,那些不会的问题也是通过网上搜别人的答案才得以解决的。所以,我就想把我看这本书的心得连带课后的解答分享给大家。同时也是给我坚持把算法导论这本书看完的一个动力 ^_^
因为本书的第一章相当于一个导论就直接跳过了,那么,从第二章开始!
第二章主要介绍了插入排序和归并排序:
所谓的插入排序就像是一局扑克刚开始时的摸牌阶段,你对手中的扑克所做的整理排序一样。开始时,我们的左手为空并且桌子上所有牌的牌面向下。然后,我们每次从桌子上摸一张牌,并把它按照一定的顺序(从大到小/从小到大)插入到左手正确的位置。每次为了找到正确的位置,我们需要从右向左将它与左手中牌进行比较。当桌子上的牌为空时,我们左手中的这副牌也就排好了。
给出代码:
//插入算法:输入n个数,升序排列 #include <stdio.h> #include <stdlib.h> void main() { //输入10个数 int nums[10] = { 55, 12, 98, 7, 24, 46, 87, 1, 67, 55 }; int key; //从1开始是因为当i = 0时,只有一张牌不用排序 for (int i = 1; i < sizeof(nums) / sizeof(int); i++) { //key相当于新摸到的牌 key = nums[i]; int j = i - 1; //将新摸到的牌key与它前面的牌进行比较,直到比key小为止 while (j >= 0 && nums[j] > key) { //如果前面的牌比key大,将前面牌的位置后移 nums[j + 1] = nums[j]; j = j - 1; } //将key插入到j+1的位置上 nums[j + 1] = key; } printf("%d %d %d %d %d %d %d %d %d %d", nums[0], nums[1], nums[2], nums[3], nums[4], nums[5], nums[6], nums[7], nums[8], nums[9]); system("pause"); }
归并排序用到的是分治法的思想,分治法指的是将原问题分解为几个规模较小但类似于原问题的子问题,递归的求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
书中的这张图能比较直观的看到归并排序的过程
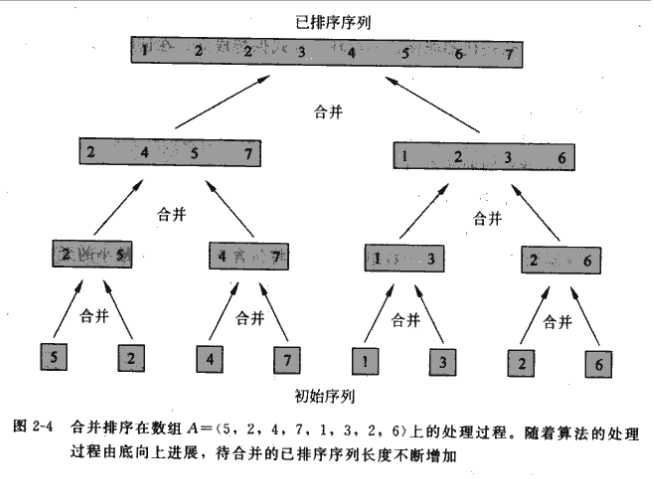
图中我们先将数组中的数据分割成一个个小的独立单元,再通过对两个独立单元的排序(如:两个独立单元5、2,合并排序后形成新的独立单元2、5,独立单元2、5和4、7,合并排序后形成新的独立单元2、4、5、7,以此类推)从而将整个数组进行排序
给出代码,这里最好的理解办法就是把代码复制到VS中,下断点一步步跟:
//归并排序 #include <stdlib.h> #include <stdio.h> #include <limits.h> void merge(int * nums, int startNum, int midNum, int lastNum) { //定义两个数组用于存储nums分割后的左半部分和右半部分 int LNums[6] = { 0 }; int RNums[6] = { 0 }; //求出左半部分的数组LNums中将会有多少个数字 int numLeft = midNum - startNum + 1; //求出右半部分的数组RNums中将会有多少个数字 int numRight = lastNum - midNum; int i; int j; //将左半部分的数放入LNums中 for (i = 0; i < numLeft; i++) { LNums[i] = nums[startNum + i]; } //将右半部分的数放入RNums中 for (j = 0; j < numRight; j++) { RNums[j] = nums[midNum + j + 1]; } //这里将数组最后一个数设置为最大值的意义是:当LNums或RNums中的一个完成排序后,可以确保另一个数组能继续正常排序 LNums[i] = INT_MAX; RNums[j] = INT_MAX; i = 0; j = 0; //对nums进行排序 for (int k = startNum; k <= lastNum; k++) { //这里相当于有左右两摞牌LNums和RNums(这里注意LNums和RNums自身已经是从小到大排好序的),每次对比两摞牌最上面的一张,选取较小的存入nums中 if (LNums[i] <= RNums[j]) { nums[k] = LNums[i]; i += 1; } else { nums[k] = RNums[j]; j += 1; } } } void merge_sort(int * nums,int startNum,int lastNum) { if (startNum < lastNum) { //取数组中点以便将数组分为左右两部分 int midNum = (startNum + lastNum) / 2; //个人理解是递归的分割左数组 merge_sort(nums, startNum, midNum); //个人理解是递归的分割右数组 merge_sort(nums, midNum + 1, lastNum); //将左右两个数组排序并合并 merge(nums, startNum, midNum, lastNum); } } void main() { int nums[10] = { 9, 6, 7, 2, 5, 4, 3, 0, 1, 8 }; merge_sort(nums, 0, 9); printf("%d %d %d %d %d %d %d %d %d %d", nums[0], nums[1], nums[2], nums[3], nums[4], nums[5], nums[6], nums[7], nums[8], nums[9]); system("pause"); }
下次将更新第二章习题部分
原文:http://www.cnblogs.com/gkarma/p/4312042.html