| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 6629 | Accepted: 3058 |
Description
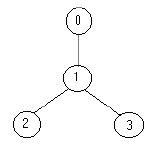
Input
Output
Sample Input
4 0:(1) 1 1:(2) 2 3 2:(0) 3:(0) 5 3:(3) 1 4 2 1:(1) 0 2:(0) 0:(0) 4:(0)
Sample Output
1 2
Source
POJ 1463:
题目意思:
在树的节点上放士兵,使得树的每一条边都有士兵看守,求所需要的最少士兵数;
解题思路:
树状dp,状态转移为:
如果这个点放了士兵,则该点的dp等于所有儿子节点放士兵或者不放士兵的最小值之和;
如果这个点不放士兵,则该点的dp等于所有儿子节点必须放士兵的和;
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cstdio> 6 #include<vector> 7 using namespace std; 8 const int maxn=1507; 9 const int inf=0x3f3f3ff; 10 struct node 11 { 12 int to,next; 13 }; 14 node tree[15007]; 15 vector<int> G[maxn]; 16 int dp[maxn][2]; 17 int n; 18 void init() 19 { 20 for(int i=0;i<maxn;i++) G[i].clear(); 21 memset(tree,0,sizeof(tree)); 22 for(int i=0;i<maxn;i++) 23 { 24 dp[i][0]=dp[i][1]=inf; 25 } 26 } 27 void dfs(int point) 28 { 29 int res1=0,res2=0; 30 for(int i=0;i<G[point].size();i++) 31 { 32 dfs(G[point][i]); 33 res1+=dp[G[point][i]][1]; 34 res2+=min(dp[G[point][i]][1],dp[G[point][i]][0]); 35 } 36 dp[point][0]=res1; 37 dp[point][1]=min(dp[point][1],res2+1); 38 } 39 int main() 40 { 41 //freopen("in.txt","r",stdin); 42 while(~scanf("%d",&n)){ 43 init(); 44 int a,b,c,root=-1; 45 for(int i=1;i<=n;i++) 46 { 47 scanf("%d:(%d)",&a,&b); 48 if(root==-1) root=a; 49 for(int j=0;j<b;j++) 50 { 51 scanf("%d",&c); 52 G[a].push_back(c); 53 } 54 } 55 dfs(root); 56 int ans=min(dp[root][1],dp[root][0]); 57 printf("%d\n",ans); 58 } 59 return 0; 60 }
原文:http://www.cnblogs.com/codeyuan/p/4312193.html