几种方法判断平面点在三角形内

最近在做一个Unity实现的3D建模软件，其中需要在模型表面进行操作的时候，需要用到点和三角形位置关系的判定算法。由于一个模型往往是几千个三角片，所以这个判定算法必须高效，否则会影响最终程序的整体性能。这里记录一下一些算法，如有误请指出，谢谢！

首先假设点和三角形在同一平面内，如果不在同一平面，需要用其它方法先筛选。

常用的几种平面点－三角形位置关系判定方法有（以下算法执行必须先保证点和三角形位于同平面）：

1.顺时针／逆时针判定法

该方法要求点的顺序是顺时针或逆时针的，如果是顺时针的点，沿着3条边走，如果目标点P在三角形内，那么P始终在边的右侧。

同理，如果是逆时针的话，目标点p应该始终在边的左侧。

例：逆时针的三个点abc，判断abXap , bcXbp , caXcp,如果这三个向量叉积的Z值都同向，并且都为负的话（左手系），说明p点在三角形内部。

向量叉积较为简单，这里不再赘述。

2.面积法

已知三角形的三点坐标，由海伦公式可以直接得到面积，只需要比较Spab+Spbc+Spca和Sabc的大小关系即可。但是由于面积公式涉及开平方根，会产生浮点数的精度问题。

3.角度法

同面积法类似，如果点在三角形内，则pa,pb,pc与ab,bc,ca,形成6个角，这6个角的和应该为180度。同样由于求角度涉及三角函数运算，效率较慢，并且有浮点数的精度问题，所以这个方法一般是不被采用的。

4.斜坐标系法

这个方法正是我主要想介绍的方法，思路来源于网上，我整理了一下，感觉效率应该是这几种方法里最快的了。

首先上图：

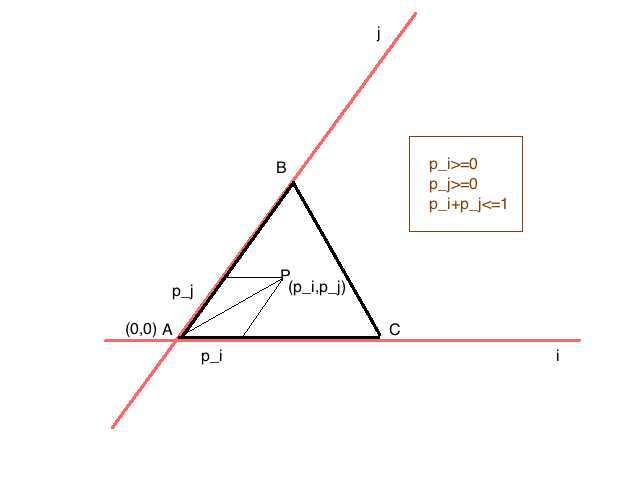
首先以AC、AB为i、j基向量，建立斜坐标系。首先得知道斜坐标系有两个性质：

1）平面向量中的结论在斜坐标系中成立。

2）直线方程求法和直角坐标系相同。

其中2）可以用直线的几何性质在斜坐标系中推导得到，具体方法和直角坐标系中推导直线方程类似，只不过多了个斜坐标系的夹角三角函数而已。

下面记AB、AP、AC、i、j均为向量，并且i＝＝AC，j＝＝AB，是斜坐标系的基向量。

且BC的直线方程为i+j=1;

设P坐标为(p_i,p_j),若要P点在三角形内,必满足  1) p_i>=0，  2) p_j>=0，  3)p_i+p_j<=1。

这里可以用向量表示为: AP=p_i*AC+p_j*AB

左右两边同乘AC、AB。可以得到两个方程。

AP•AC=p_i*(AC•AC)+p_j(AB•AC)    -----1

AP•AB=p_i*(AC•AB)+p_j*(AB•AB)  -----2

 由这两个方程可以得到：

p_i=((AP•AC)*(AB•AB)-(AP•AB)*(AC•AB))/((AC•AC)*(AB•AB)-(AC•AB)*(AC•AB));

p_j=((AP•AB)*(AC•AC)-(AP•AC)*(AB•AC))/((AC•AC)*(AB•AB)-(AC•AB)*(AC•AB));

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

至此已经能够判断点是否在三角形内，下面可以借助柯西不等式，避免作浮点数除法，改为减法。

由柯西不等式的向量形式可以得到：

(AC•AC)*(AB•AB)>=(AC•AB)*(AC•AB)恒成立，所以分母不会为负，我们只需要判断分子的正负即可。

即，判断p_i>=0 , p_j>=0，等价于：

(AP•AC)*(AB•AB)-(AP•AB)*(AC•AB)>=0  ,(AP•AB)*(AC•AC)-(AP•AC)*(AB•AC)>=0,

并且p_i+p_j<=1，可以两边同乘以分母，避免了浮点数的除法运算，即如下式：

((AP•AC)*(AB•AB)-(AP•AB)*(AC•AB))+((AP•AB)*(AC•AC)-(AP•AC)*(AB•AC))-((AC•AC)*(AB•AB)-(AC•AB)*(AC•AB))<=0

代码如下：

 1     static public bool pointInTriangle(Vector3 p,Vector3 a,Vector3 b,Vector3 c)
 2     {
 3         if(pointInTrianglePlane(p,a,b,c)==false)
 4             return false;
 5         Vector3 AC=c-a;
 6         Vector3 AB=b-a;
 7         Vector3 AP=p-a;
 8 
 9         float f_i=Vector3.Dot(AP,AC)*Vector3.Dot(AB,AB)-Vector3.Dot(AP,AB)*Vector3.Dot(AC,AB);
10         float f_j=Vector3.Dot(AP,AB)*Vector3.Dot(AC,AC)-Vector3.Dot(AP,AC)*Vector3.Dot(AB,AC);
11         float f_d=Vector3.Dot(AC,AC)*Vector3.Dot(AB,AB)-Vector3.Dot(AC,AB)*Vector3.Dot(AC,AB);
12         if(f_d<0) Debug.Log("erro f_d<0");
13         //p_i==f_i/f_d
14         //p_j==f_j/f_d
15         if(f_i>=0 && f_j>=0 && f_i+f_j-f_d<=0)
16             return true;
17         else
18             return false;
19     }

几种方法判断平面点在三角形内

原文：http://www.cnblogs.com/kyokuhuang/p/4314173.html