上一回我们已经将所有有问题的相亲情况表剔除了,那么接下来要做的就是安排相亲了。因为过年时间并不是很长,所以姑姑希望能够尽可能在一天安排比较多的相亲。由于一个人同一天只能和一个人相亲,所以要从当前的相亲情况表里选择尽可能多的组合,且每个人不会出现两次。不知道有没有什么好办法,对于当前给定的相亲情况表,能够算出最多能同时安排多少组相亲呢?
同样的,我们先将给定的情况表转换成图G=(V,E)。在上一回中我们已经知道这个图可以被染成黑白两色。不妨将所有表示女性的节点记为点集A,表示男性的节点记为点集B。则有A∪B=V。由问题可知所有边e的两个端点分别属于AB两个集合。则可以表示成如下的图:
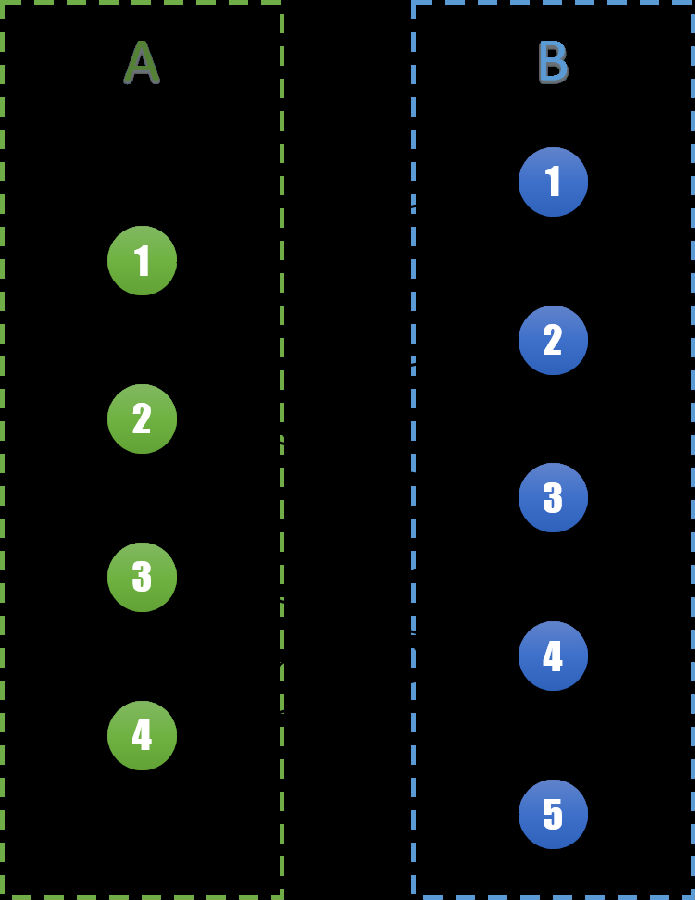
同样的,我们将所有的边分为两个集合。集合S和集合M,同样有S∪M=E。边集S表示在这一轮相亲会中将要进行的相亲,边集M表示在不在这一次进行。对于任意边(u,v) ∈ S,我们称u和v为一组匹配,它们之间相互匹配。在图G,我们将边集S用实线表示,边集M用虚线表示。得到下图:
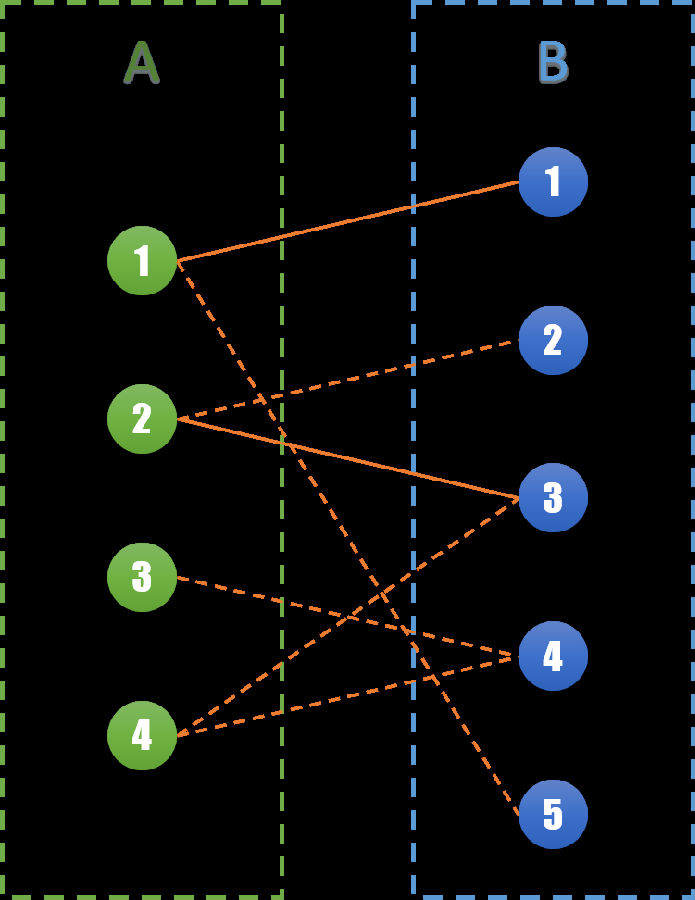
则原问题转化为,最多能选择多少条边到集合S,使得S集合中任何两条边不相邻(即有共同的顶点)。显然的,|S|<=Min{|A|, |B|}。
那么能不能找到一个算法,使得能够很容易计算出尽可能多的边能够放入集合S?我们不妨来看一个例子:

对于已经匹配的点我们先不考虑,我们从未匹配的点来做。这里我们选择A集合中尚未匹配的点(A3和A4)考虑:
对于A3点,我们可以发现A3与B4右边相连,且都未匹配。则直接将(A3,B4)边加入集合S即可。
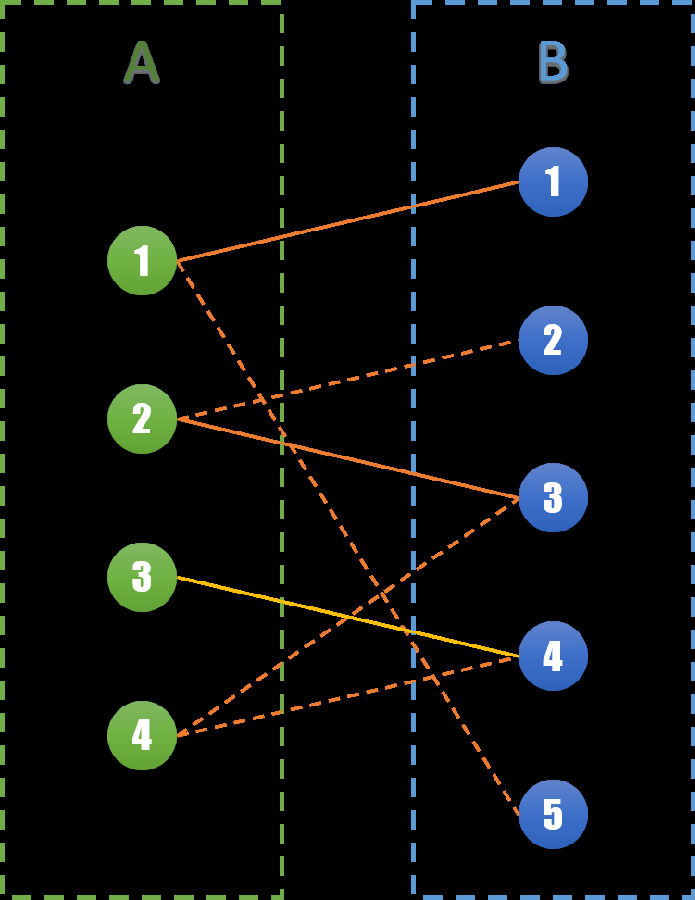
对于A4点,我们发现和A4相连的B3,B4点都已经匹配了。但是再观察可以发现,如果我们将A2和B2相连,则可以将B3点空出来。那么就可以同时将(A2,B2),(A4,B3)相连。将原来的一个匹配变成了两个匹配。
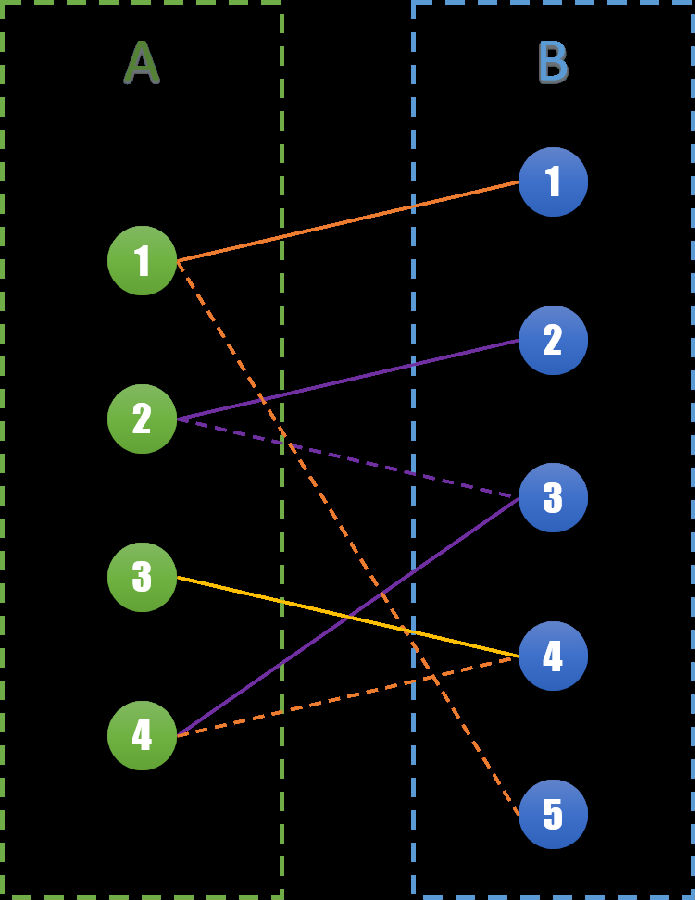
让我们来仔细看看这一步:我们将这次变换中相关联的边标记出来,如下图所示紫色的3条边(A2,B2),(A2,B3),(A4,B3)。
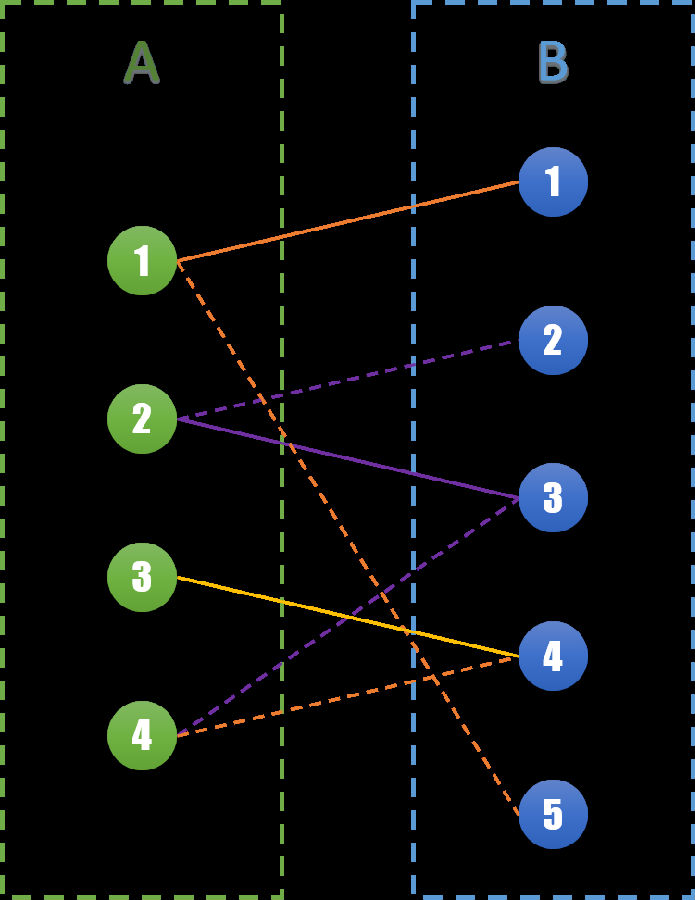
这三条边构成了一条路径,可以发现这条路径有个非常特殊的性质。虚线和实线相互交错,并且起点和终点都是尚未匹配的点,且属于两个不同的集合。我们称这样的路径为交错路径。
再进一步分析,对于任意一条交错路径,虚线的数量一定比实线的数量多1。我们将虚线和实线交换一下,就变成了下面的图:
在原来1个匹配的基础上,我们得到了2个新的匹配,S集合边的数量也增加了1。并且原来在已经匹配的点仍然是已经匹配的状态。
再回头看看A3点匹配时的情况:对于(A3,B4)这一条路径,同样满足了交错路径的性质。
至此我们得到了一个找新匹配的有效算法:
选取一个未匹配的点,查找是否存在一条以它为起点的交错路径。若存在,将该交错路径的边虚实交换。否则在当前的情况下,该点找不到可以匹配的点。
又有对于已经匹配的点,该算法并不会改变一个点的匹配状态。所以当我们对所有未匹配的点都计算过后,仍然没有交错路径,则不可能找到更多的匹配。此时S集合中的边数即为最大边数,我们称为最大匹配数。
那么我们再一次梳理整个算法:
1. 依次枚举每一个点i;
2. 若点i尚未匹配,则以此点为起点查询一次交错路径。
最后即可得到最大匹配数。
在这个基础上仍然有两个可以优化的地方:
1.对于点的枚举:当我们枚举了所有A中的点后,无需再枚举B中的点,就已经得到了最大匹配。
2.在查询交错路径的过程中,有可能出现Ai与Bj直接相连,其中Bj为已经匹配的点,且Bj之后找不到交错路径。之后又通过Ai查找到了一条交错路径{Ai,Bx,Ay,…,Az,Bj}延伸到Bj。由于之前已经计算过Bj没有交错路径,若此时再计算一次就有了额外的冗余。所以我们需要枚举每个Ai时记录B集合中的点是否已经查询过,起点不同时需要清空记录。
第1行:2个正整数,N,M(N表示点数 2≤N≤1,000,M表示边数1≤M≤5,000)
第2..M+1行:每行两个整数u,v,表示一条无向边(u,v)
第1行:1个整数,表示最大匹配数
5 4 3 2 1 3 5 4 1 5
2
解题:最大匹配

1 /* 2 @author: Lev 3 @date: 4 */ 5 #include <iostream> 6 #include <cstdio> 7 #include <cmath> 8 #include <cstring> 9 #include <string> 10 #include <cstdlib> 11 #include <algorithm> 12 #include <map> 13 #include <set> 14 #include <queue> 15 #include <climits> 16 #include <deque> 17 #include <sstream> 18 #include <fstream> 19 #include <bitset> 20 #include <iomanip> 21 #define LL long long 22 #define INF 0x3f3f3f3f 23 24 using namespace std; 25 const int maxn = 1010; 26 vector<int>g[maxn]; 27 int link[maxn]; 28 bool used[maxn]; 29 bool dfs(int u){ 30 for(int i = g[u].size()-1; i >= 0; --i){ 31 if(!used[g[u][i]]){ 32 used[g[u][i]] = true; 33 if(link[g[u][i]] == -1 || dfs(link[g[u][i]])){ 34 link[g[u][i]] = u; 35 link[u] = g[u][i]; 36 return true; 37 } 38 } 39 } 40 return false; 41 } 42 int main(){ 43 int n,m; 44 while(~scanf("%d %d",&n,&m)){ 45 for(int i = 0; i < maxn; ++i){ 46 g[i].clear(); 47 link[i] = -1; 48 } 49 for(int i = 0; i < m; ++i){ 50 int u,v; 51 scanf("%d %d",&u,&v); 52 g[u].push_back(v); 53 g[v].push_back(u); 54 } 55 int ans = 0; 56 for(int i = 1; i <= n; ++i) 57 if(link[i] == -1){ 58 memset(used,false,sizeof(used)); 59 ans += dfs(i); 60 } 61 printf("%d\n",ans); 62 } 63 return 0; 64 }
hihoCoder #1122 : 二分图二?二分图最大匹配之匈牙利算法
原文:http://www.cnblogs.com/crackpotisback/p/4321050.html