这道题又一次更新了我的世界观与人生观Orz……最开始我是设计了一个O(n)的递推算法,本以为可以轻松AC没想到居然TLE了……然后搜了一下题解,才发现这道题要用矩阵的思想去做。
通过对题目的分析,我们可以得到矩阵递推公式如下:
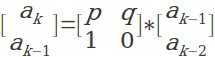
将公式右边推至a1,a0即可得:
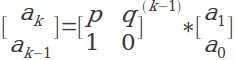
然后这个题的关键就转化成了求[p q;1 0]的(k-1)次幂的问题。
接下来求矩阵的幂可以用快速幂运算来解决,这样就将O(n)的算法化简为了O(logn)的复杂度,如此一来就可以AC了。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 |
#include <stdio.h>#include<stdlib.h>#include<string.h>#define NUM 10000typedef
long long ll;typedef
struct{ ll num[2][2];}Matrix;ll a1,a0,p,q,k;Matrix mul(Matrix a1,Matrix a2){ Matrix solution; int
i,j; for(i=0;i<=1;i++) for(j=0;j<=1;j++) { solution.num[i][j]=(a1.num[i][0]*a2.num[0][j]+a1.num[i][1]*a2.num[1][j])%NUM; } return
solution;}Matrix a,res;void
calculate(ll n){ res.num[0][0]=1; res.num[1][1]=1; res.num[1][0]=0; res.num[0][1]=0; while(n) { if(n&1) res=mul(res,a); n>>=1; a=mul(a,a); } ll n1=(res.num[0][0]*a1+res.num[0][1]*a0)%NUM; //ll n2=(res.num[1][0]*a1+res.num[1][1]*a0)%NUM; printf("%lld\n",n1);}int
main(){ ll i,j; while(scanf("%lld%lld%lld%lld%lld",&a0,&a1,&p,&q,&k)!=EOF) { if(k==0) { printf("%lld\n",a0%NUM); } else
if(k==1) { printf("%lld\n",a1%NUM); } else { a.num[0][0]=p; a.num[0][1]=q; a.num[1][0]=1; a.num[1][1]=0; calculate(k-1); } } return
0;} |
关于矩阵的快速幂运算,可以参考这篇博文:http://www.cnblogs.com/yan-boy/archive/2012/11/29/2795294.html
原文:http://www.cnblogs.com/wickedpriest/p/3588268.html