排序是数据处理中经常使用的一种重要运算,在计算机及其应用系统中,花费在排序上的时间在系统运行时间中占有很大比重;并且排序本身对推动算法分析的发展也起很大作用。
1.排序或分类
所谓排序,就是要整理文件中的记录,使之按关键字递增(或递减)次序排列起来。其确切定义如下:
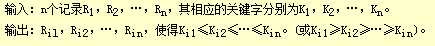
1)被排序对象--文件
记录则由若干个数据项(或域)组成。其中有一项可用来标识一个记录,称为关键字项。该数据项的值称为关键字(Key)。
注意:
在不易产生混淆时,将关键字项简称为关键字。
2)排序运算的依据--关键字
2.排序的稳定性
在待排序的文件中,若存在多个关键字相同的记录,经过排序后这些具有相同关键字的记录之间的相对次序保持不变,该排序方法是稳定的;若具有相同关键字的记录之间的相对次序发生变化,则称这种排序方法是不稳定的。
3.排序方法的分类
1)按是否涉及数据的内、外存交换分
在排序过程中,若整个文件都是放在内存中处理,排序时不涉及数据的内、外存交换,则称之为内部排序(简称内排序);反之,若排序过程中要进行数据的内、外存交换,则称之为外部排序。
注意: ① 内排序适用于记录个数不很多的小文件
② 外排序则适用于记录个数太多,不能一次将其全部记录放人内存的大文件。`
2)按策略划分内部排序方法
可以分为五类:插入排序、选择排序、交换排序、归并排序和分配排序。
3.排序算法分析
1)排序算法的基本操作
大多数排序算法都有两个基本的操作:
2)待排文件的常用存储方式
以顺序表(或直接用向量)作为存储结构
排序过程:对记录本身进行物理重排(即通过关键字之间的比较判定,将记录移到合适的位置)
以链表作为存储结构 排序过程:无须移动记录,仅需修改指针。通常将这类排序称为链表(或链式)排序;
用顺序的方式存储待排序的记录,但同时建立一个辅助表(如包括关键字和指向记录位置的指针组成的索引表)
排序过程:只需对辅助表的表目进行物理重排(即只移动辅助表的表目,而不移动记录本身)。适用于难于在链表上实现,仍需避免排序过程中移动记录的排序方法。
3)排序算法性能比较
评价排序算法好坏的标准主要有两条:
① 执行时间和所需的辅助空间
② 算法本身的复杂程度
1.直接插入排序
2.希尔排序
基本思想:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
算法描述:动画演示过程
1.冒泡排序
2.快速排序
1.直接选择排序
2.堆排序
基本思想:堆排序(HeapSort)是一树形选择排序。堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]重新恢复堆,重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。
算法描述:动画演示过程

1 ///Name:Tree 2 ///Author:JA 3 ///Date:2015-3-11 4 5 6 7 ///对顺序表L作直接插入排序 8 void InsertSort(SqList *L){ 9 for (i = 2; i <= L.length;++i) 10 if (LT(L.r[i].key, L.[r - 1].key)){ //将L.r[i]插入有序集表 11 L.r[0] = L.r[i]; 12 L.r[i] = L.r[i - 1]; 13 for (j = i - 2; LT(L.r[0].key, L.r[j].key); --j) 14 L.r[j + 1] = L.r[j]; //记录后移 15 L.r[j + 1] = L.r[j]; //插入到正确位置 16 } 17 }//InsertSort 18 19 //希尔排序 20 void ShellPass(SeqList R,int d) 21 {//希尔排序中的一趟排序,d为当前增量 22 for (i = d + 1; i <= n; i++) //将R[d+1..n]分别插入各组当前的有序区 23 if (R[i].key<R[i - d].key){ 24 R[0] = R[i]; j = i - d; //R[0]只是暂存单元,不是哨兵 25 do {//查找R[i]的插入位置 26 R[j + d]; = R[j]; //后移记录 27 j = j - d; //查找前一记录 28 } while (j>0 && R[0].key < R[j].key); 29 R[j + d] = R[0]; //插入R[i]到正确的位置上 30 } //endif 31 } //ShellPass 32 void ShellSort(SeqList R) 33 { 34 int increment = n; //增量初值,不妨设n>0 35 do { 36 increment = increment / 3 + 1; //求下一增量 37 ShellPass(R,increment); //一趟增量为increment的Shell插入排序 38 } while (increment>1) 39 } //ShellSort 40 41 //冒泡排序 42 void BubbleSort(SeqList R) 43 { //R(l..n)是待排序的文件,采用自下向上扫描,对R做冒泡排序 44 int i,j; 45 Boolean exchange; //交换标志 46 for (i = 1; i<n; i++){ //最多做n-1趟排序 47 exchange = FALSE; //本趟排序开始前,交换标志应为假 48 for (j = n - 1; j >= i; j--) //对当前无序区R[i..n]自下向上扫描 49 if (R[j + 1].key<R[j].key){//交换记录 50 R[0] = R[j + 1]; //R[0]不是哨兵,仅做暂存单元 51 R[j + 1] = R[j]; 52 R[j] = R[0]; 53 exchange = TRUE; //发生了交换,故将交换标志置为真 54 } 55 if (!exchange) //本趟排序未发生交换,提前终止算法 56 return; 57 } //endfor(外循环) 58 } //BubbleSort 59 60 //快速排序 61 void QuickSort(SeqList R,,int low,int high) 62 { //对R[low..high]快速排序 63 int pivotpos; //划分后的基准记录的位置 64 if (low<high){//仅当区间长度大于1时才须排序 65 pivotpos = Partition(R,low,high); //对R[low..high]做划分 66 QuickSort(R,low,pivotpos - 1); //对左区间递归排序 67 QuickSort(R,pivotpos + 1,high); //对右区间递归排序 68 } 69 } //QuickSort 70 int Partition(SeqList R,int i,int j) 71 {//调用Partition(R,low,high)时,对R[low..high]做划分, 72 //并返回基准记录的位置 73 ReceType pivot = R[i]; //用区间的第1个记录作为基准 ‘ 74 while (i<j){ //从区间两端交替向中间扫描,直至i=j为止 75 while (i < j&&R[j].key >= pivot.key) //pivot相当于在位置i上 76 j--; //从右向左扫描,查找第1个关键字小于pivot.key的记录R[j] 77 if (i < j) //表示找到的R[j]的关键字<pivot.key 78 R[i++] = R[j]; //相当于交换R[i]和R[j],交换后i指针加1 79 while (i < j&&R[i].key <= pivot.key) //pivot相当于在位置j上 80 i++; //从左向右扫描,查找第1个关键字大于pivot.key的记录R[i] 81 if (i<j) //表示找到了R[i],使R[i].key>pivot.key 82 R[j--] = R[i]; //相当于交换R[i]和R[j],交换后j指针减1 83 } //endwhile 84 R[i] = pivot; //基准记录已被最后定位 85 return i; 86 } //partition 87 88 //直接选择排序 89 void SelectSort(SeqList R) 90 { 91 int i,j,k; 92 for (i = 1; i<n; i++){//做第i趟排序(1≤i≤n-1) 93 k = i; 94 for (j = i + 1; j <= n; j++) //在当前无序区R[i..n]中选key最小的记录R[k] 95 if (R[j].key<R[k].key) 96 k = j; //k记下目前找到的最小关键字所在的位置 97 if (k != i){ //交换R[i]和R[k] 98 R[0] = R[i]; R[i] = R[k]; R[k] = R[0]; //R[0]作暂存单元 99 } //endif 100 } //endfor 101 } //SeleetSort 102 103 //堆排序 104 void HeapSort(SeqIAst R) 105 { //对R[1..n]进行堆排序,不妨用R[0]做暂存单元 106 int i; 107 BuildHeap(R); //将R[1-n]建成初始堆 108 for (i = n; i > 1; i--){ //对当前无序区R[1..i]进行堆排序,共做n-1趟。 109 R[0] = R[1]; R[1] = R[i]; R[i] = R[0]; //将堆顶和堆中最后一个记录交换 110 Heapify(R,1,i - 1); //将R[1..i-1]重新调整为堆,仅有R[1]可能违反堆性质 111 } //endfor 112 } //HeapSort
3/13/2015 2:35:47 PM
原文:http://www.cnblogs.com/joeaaron007/p/4335306.html