Cordic 算法之 反正切

在通信的算法中，常采用Cordic算法求反正切:Angle  = artan(y/x)。

及给定x,y 的坐标通过向量旋转，使得y--〉0， 通过不断地迭代使得 y 逐渐 趋渐0；

最终得到旋转的角度 z, z 即为 反正切值。

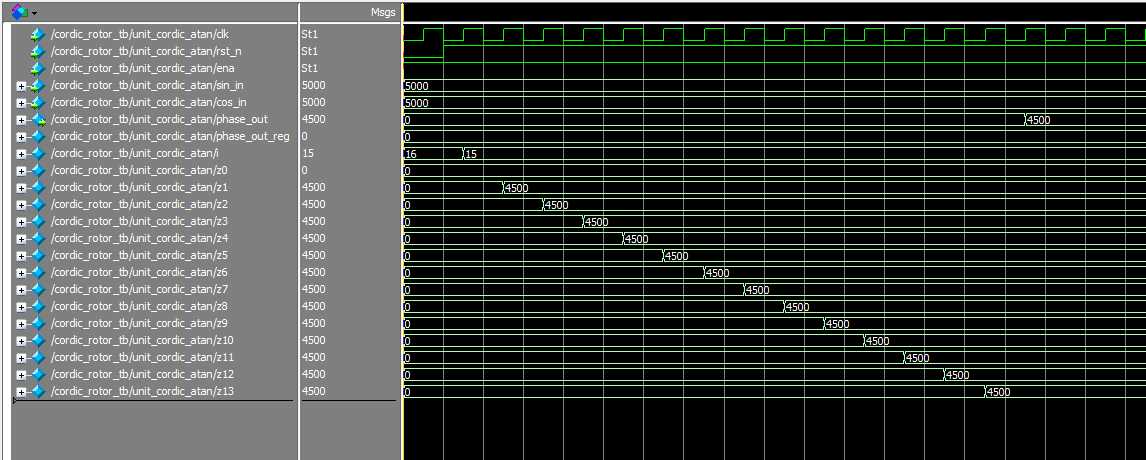
验证 输入y=5000, x=5000;通过计算 atan(5000/5000) =0.5（pi 弧度）*90度 = 45度。

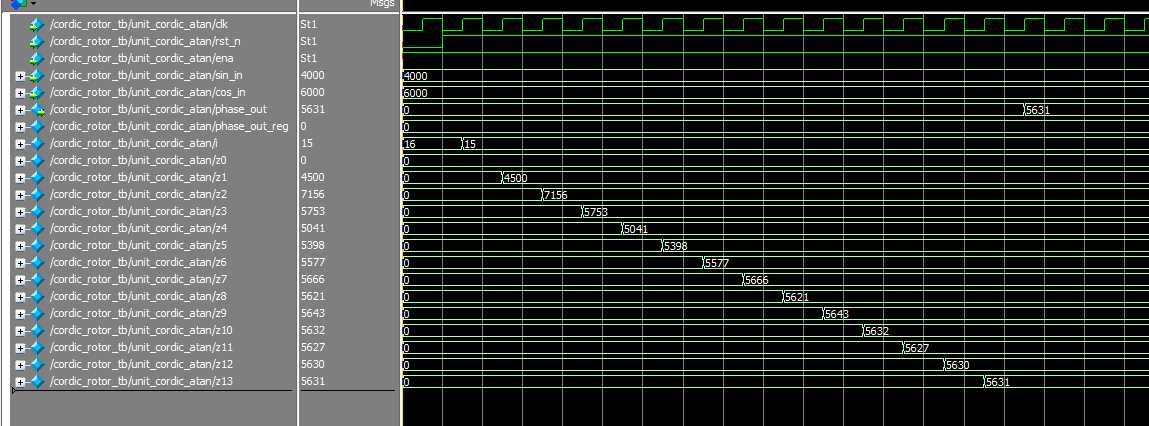
验证 输入y=6000, x=4000;通过计算 atan(6000/4000) =0.626（pi 弧度）* 90度 = 56.3度

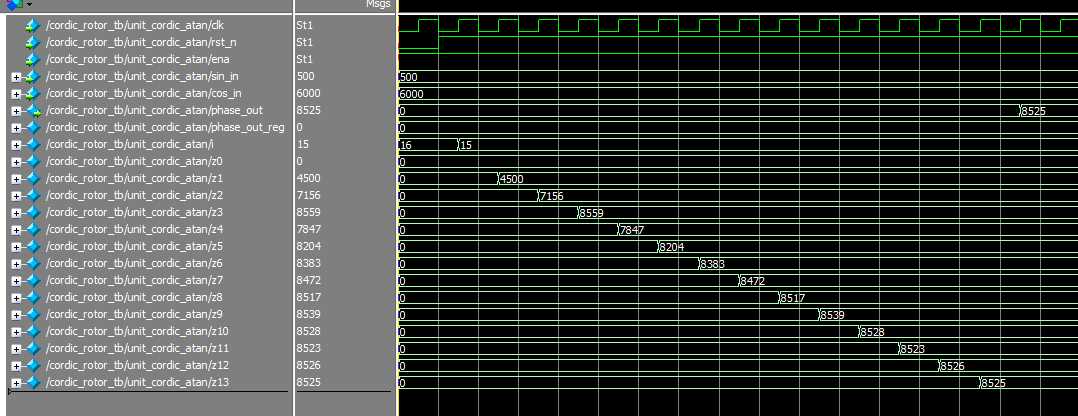
验证 输入y=6000, x=500;通过计算 atan(6000/0500) =0.947（pi 弧度）* 90度 = 85.23度。

//level 1
always@(posedge clk or negedge rst_n)
begin
        if(!rst_n)
               begin
                       x1<=0;
                       y1<=0;
                       z1<=0;
               end
         else
                if(ena)
                       if(y0<0)
                               begin
                                      x1<=x0-y0;
                                      y1<=y0+x0;
                                      z1<=z0-15‘d4500;  //45deg
                               end
                      else if(y0>0)
                               begin
                                      x1<=x0+y0;
                                      y1<=y0-x0;
                                      z1<=z0+15‘d4500;  //45deg 
                              end 
                      else 
                          begin
                              x1 <= x0;
                              y1 <= y0;
                              z1 <= z0;
                          end 
end

//level 2
always@(posedge clk or negedge rst_n)
begin
        if(!rst_n)
               begin
                       x2<=0;
                       y2<=0;
                       z2<=0;
               end
         else
                if(ena)
                       if(y1<0)
                               begin
                                      x2<=x1-{y1[DATA_WIDTH-1],y1[DATA_WIDTH-1:1]};
                                      y2<=y1+{x1[DATA_WIDTH-1],x1[DATA_WIDTH-1:1]};
                                      z2<=z1-15‘d2656;  //26.56deg
                                     
                               end
                        else if(y1>0)
                               begin
                                      x2<=x1+{y1[DATA_WIDTH-1],y1[DATA_WIDTH-1:1]};
                                      y2<=y1-{x1[DATA_WIDTH-1],x1[DATA_WIDTH-1:1]};
                                      z2<=z1+15‘d2656;
                               end
                      else
                               begin
                                 x2 <= x1;
                                 y2 <= y1;
                                 z2 <= z1;
                                 end
end

...

...

...

//level 13
always@(posedge clk or negedge rst_n)
begin
        if(!rst_n)
                 begin
                       x13<=0;
                       y13<=0;
                       z13<=0;
               end
         else
                if(ena)
                       if(y12<0)
                               begin
                                      x13<=x12-{{12{y12[DATA_WIDTH-1]}},y12[DATA_WIDTH-1:12]};
                                      y13<=y12+{{12{x12[DATA_WIDTH-1]}},x12[DATA_WIDTH-1:12]};
                                      z13<=z12-15‘d01;  //0.014deg
                               end
                        else if(y12>0)
                              begin
                                      x13<=x12+{{12{y12[DATA_WIDTH-1]}},y12[DATA_WIDTH-1:12]};
                                      y13<=y12-{{12{x12[DATA_WIDTH-1]}},x12[DATA_WIDTH-1:12]};
                                      z13<=z12+15‘d01;
                               end
                             else
                               begin
                                    x13 <= x12;
                                    y13 <= y12;
                                    z13 <= z12;
                                 end
end

Cordic 算法之 反正切,布布扣,bubuko.com

Cordic 算法之 反正切

原文：http://www.cnblogs.com/touchblue/p/3590459.html