hdu1054Strategic Game(树形DP)

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree:



the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

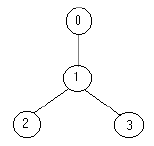
1
2
解题：在一棵树上的每一个点，只存在放与不放两种情况，那么当根不放时，则根的孩子节点是必须放的情况，如果根不放时，则根的孩子可以放也可以不放。
	公式： dp[p][0]+=dp[child][1];  dp[p][1]=min(dp[p][1]+dp[child][0],dp[p][1]+dp[child][1]);  p:根节点   child:p的子节点
#include<stdio.h>
#include<string.h>
#define inf 99999
struct nnn
{
    int k;
    int son[1505];
}node[1505];
int dp[1505][2],vist[1505],n;
int min(int a,int b)
{
    return a>b?b:a;
}
void dfs(int p)
{
    dp[p][0]=0;dp[p][1]=1; vist[p]=1;
    for(int k=1;k<=node[p].k;k++)
    {
        int child=node[p].son[k];
        if(vist[child])continue;//区分根节点与子节点，这样不会形成循环
        dfs(child);
        dp[p][0]+=dp[child][1];
        dp[p][1]=min(dp[p][1]+dp[child][0],dp[p][1]+dp[child][1]);
    }
}
int main()
{
    int p,num,child,sum;
    while(scanf("%d",&n)==1)
    {
        memset(vist,0,sizeof(vist));
        for(int i=0;i<n;i++)
        node[i].k=0;
        for(int i=0;i<n;i++)
        {
            scanf("%d:(%d)",&p,&num);
            int k;
            while(num--)
            {
                scanf("%d",&child);
                node[p].k++; k=node[p].k; node[p].son[k]=child;
                node[child].k++; k=node[child].k; node[child].son[k]=p;
            }
        }
        dfs(0);
        sum=dp[0][0];
        if(sum>dp[0][1]) 
        sum=dp[0][1];
        printf("%d\n",sum);
    }
}