一个整数数组,元素取值可能是1~N(N是一个较大的正整数)中的任意一个数,相同数值不会重复出现。设计一个算法,找出数列中符合条件的数对,满足数对中两数的和等于N+1。
方法一:蛮力法。这是最简单的方法,枚举出数组中所有可能的数对,看其和是否为N+1,如果是,则输出。但这种方法一般效率不高。代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 |
#include "stdafx.h"#include <stdio.h>int findCouple(int
a[], int
n, int
&val){ if
(a == NULL || n <= 0) return
-1; int
max = a[0]; for
(int m = 1; m < n; m++) { if
(a[m]>max) max = a[m]; } for
(int i = 0; i < n; i++) { for
(int j = i+1; j < n; j++) { if
(a[i] + a[j] == max + 1 && a[i] != a[j]) val++; } } return
val;}void
main(){ int
a[] = { 1, 2, 3, 4, 5 }; int
len = sizeof(a) / sizeof(int); int
val = 0; printf("%d", findCouple(a, len, val)); getchar();} |
方法二:先对数组进行排序,然后使用二分查找法,用两个指示器front和back分别指向第一个和最后一个元素,然后从两端同时向中间遍历,直到两个指针交叉。
(1)如果A[front]+A[back]>N+1,则back- -。
(2)如果A[front]+A[back]=N+1,则计数器加1,back--,同时front++。
(3)如果A[front]+A[back]<N+1,则front++。
重复上述步骤,O(n)时间就可以找到所有数对。
程序代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 |
#include "stdafx.h"#include <stdio.h>void
FixedSum(int* a, int
n, int
d){ if
(a == NULL || n <= 0) printf("数组中无元素,找个毛啊。"); else { for
(int i = 0, j = n - 1; i < n&&j >= 0 && i < j;) { if
(a[i] + a[j] < d) i++; else
if (a[i] + a[j] == d) { printf("%d,%d\n", a[i], a[j]); i++; j--; } else j--; } } }int
main(){ int
array[] = { 1, 2, 3, 4, 5 }; int
len = sizeof(array) / sizeof(array[0]); FixedSum(array, len, 6); getchar(); return
0;} |
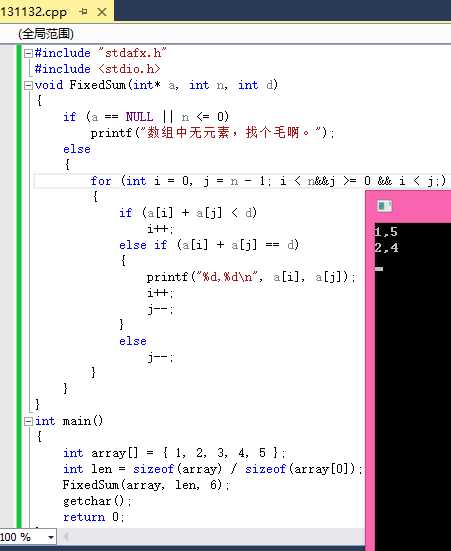
效果如图:
原文:http://www.cnblogs.com/cysolo/p/3591301.html