(1) sigmoid 函数的一般形式:
(2) sigmoid 函数的图形:
(3) 预测函数 : 



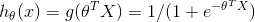
比如说有一个样本x, 他有10个 features : 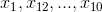 ,根据可以得到他们的预测函数的值:
,根据可以得到他们的预测函数的值:
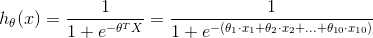
那么就可以知道样本X 的归属 : 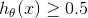 是一类, 否则是另一类。
是一类, 否则是另一类。
注意:这里假设线性边界情况 : 即形如 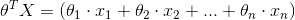 , 而不会是
, 而不会是 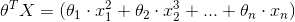 这种。而且推导也是基于这个假设的。
这种。而且推导也是基于这个假设的。
(1) 首先注意到 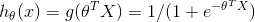 的函数值域位于 [0,1],类别分为 0,1 两类。
的函数值域位于 [0,1],类别分为 0,1 两类。
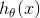 越接近于1,样本属于类别1 的可能性越大;否则,
越接近于1,样本属于类别1 的可能性越大;否则,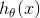 越远离1,样本属于类别0 的可能性就越大。
越远离1,样本属于类别0 的可能性就越大。
所以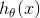 可以看做是给定样本 X 的 features ,并已知参数θ,该样本属于类别1 的概率:
可以看做是给定样本 X 的 features ,并已知参数θ,该样本属于类别1 的概率:
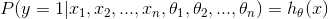 ,其中样本的归属类别用 y 来表示。
,其中样本的归属类别用 y 来表示。
(2) y 满足二项分布
.gif)
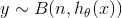
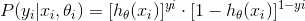
(3) 根据 MLE
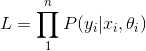
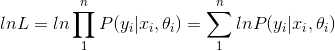
(3) 定义新的函数:
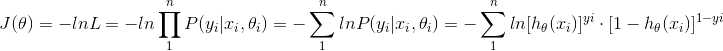
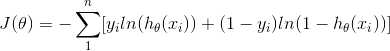
(4) 推导,求 J(θ) 对 feature j 的偏导
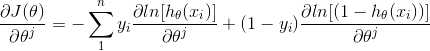
定义 A, 和 B
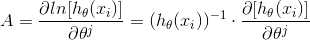
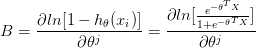
所以:
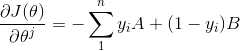
(5) 推导 A,B
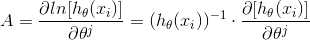
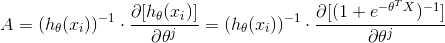
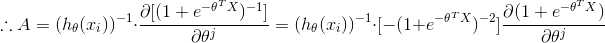
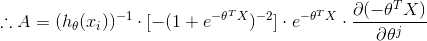
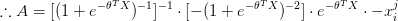
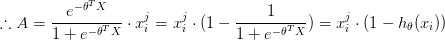
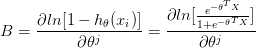
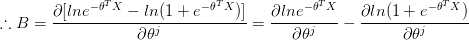
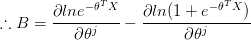
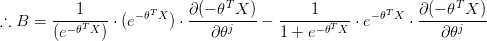
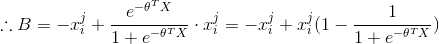
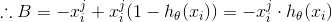
(6) 最后
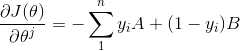
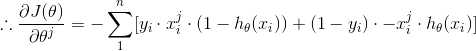
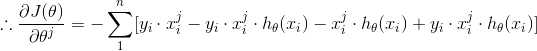
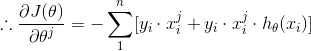
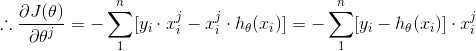
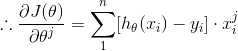
原文:http://www.cnblogs.com/happylong/p/4354810.html