1 """ 2 最近邻算法:从任一城市开始,总是选择还未参观的城市中最近的那座,再选择路径中最短的那条 3 具体如下: 4 1. 从未参观的城市中选择距离当前路径最近的城市C 5 2. 将C添加到路径末尾,并从未参观的城市中移除C 6 """ 7 8 def nn_tsp(cities): 9 start = first(cities) 10 tour = [start] 11 unvisited = set(cities - {start}) 12 while unvisited: 13 C = nearest_neighbor(tour[-1], unvisited) 14 tour.append(C) 15 unvisited.remove(C) 16 return tour 17 18 def nearest_neighbor(A, cities): 19 """ 20 寻找cities中距离城市A最近的城市 21 :param A: 22 :param cities: 23 :return: 24 """ 25 return min(cities, key=lambda c:distance(c, A)) 26 27 """ 28 虽然近似算法的速度很快,但是得到的却不是最短的距离 29 搞清楚nn_tsp的起始城市,可能会有助于我们明白它为什么会“出错” 30 """ 31 32 def plot_tour(tour): 33 """ 34 将起始的城市标记为红色 35 :param tour: 36 :return: 37 """ 38 start = tour[0] 39 plot_lines(list(tour) + [start]) 40 plot_lines([start], ‘rs‘) 41 42 def length_ratio(cities): 43 """ 44 计算nn_tsp与alltours_tsp路径长度的比值 45 :param cities: 46 :return: 47 """ 48 return tour_length(nn_tsp(cities)) / tour_length(alltours_tsp(cities)) 49 50 """ 51 优化:nn_tsp固定了起始城市,很可能使得更优值丢失 52 我们可以重复该算法,计算以任一城市为起点的最近邻算法的解,从中选择最优 53 """ 54 def repeated_nn_tsp(cities): 55 return shortest_tour(nn_tsp(cities, start) 56 for start in cities) 57 58 59 def nn_tsp(cities, start=None): 60 if start is None: 61 start = first(cities) 62 63 tour = [start] 64 unvisited = set(cities - {start}) 65 while unvisited: 66 C = nearest_neighbor(tour[-1], unvisited) 67 tour.append(C) 68 unvisited.remove(C) 69 return tour 70 71 """ 72 比较nn_tsp与repeat_nn_tsp 73 plot_tsp(nn_tsp, cities(100)) 74 plot_tsp(repeated_nn_tsp, cities(100)) 75 100 city tour with length 6734.1 in 0.004 secs for nn_tsp 76 100 city tour with length 5912.6 in 0.485 secs for repeated_nn_tsp 77 显然repeat_nn_tsp比nn_tsp表现的更好,但是,如果当城市的个数n很大时,我们就要重复n次, 78 有木有一种方法能够改进这种repeat的方式————只是穷尽部分而不是全部的城市 79 """ 80 def repeated_nn_tsp(cities, repetitions=100): 81 return shortest_tour(nn_tsp(cities, start) 82 for start in sample(cities, repetitions)) 83 84 def sample(population, k, seed=42): 85 """ 86 从population中选择k个元素作为一个样本 87 :param population: 88 :param k: 89 :param seed: 90 :return: 91 """ 92 if k is None or k > len(population): 93 return population 94 random.seed(len(population) * k * seed) 95 return random.sample(population, k) 96 97 """ 98 """ 99 def Maps(num_maps, num_cities): 100 """ 101 102 :param num_maps: 103 :param num_cities: 104 :return: 105 """ 106 return tuple(cities(num_cities, seed=(m, num_cities)) 107 for m in range(num_maps)) 108 109 """ 110 111 """ 112 def memoize(func): 113 """ 114 缓存结果 115 :param func: 116 :return: 117 """ 118 cache = {} 119 def new_func(*args): 120 try: 121 # 判断,如果之前已经运算过该函数,则返回之前的值 122 return cache[args] 123 except TypeError: 124 # 如果args无法hash,则计算该函数并返回值 125 return func(*args) 126 except KeyError: 127 # 如果args可哈希,计算该函数并存储 128 cache[args] = func(*args) 129 return cache[args] 130 new_func._cache = cache 131 new_func.__doc__ = func.__doc__ 132 new_func.__name__ = func.__name__ 133 return new_func 134 135 136 137 @memoize 138 def benchmark(function, inputs): 139 """ 140 在所有的input上运行, 返回(平均时耗,结果) 141 :param function: 142 :param inputs: 143 :return: 144 """ 145 t0 = time.clock() 146 results = list(map(function, inputs)) 147 t1 = time.clock() 148 average_time = (t1 - t0) / len(inputs) 149 return (average_time, results) 150 151 def benchmarks(tsp_algorithms, maps=Maps(30,60)): 152 """ 153 同时计算多种算法 154 :param tsp_algorithms: 155 :param maps: 156 :return: 157 """ 158 for tsp in tsp_algorithms: 159 time, results = benchmark(tsp, maps) 160 lengths = map(tour_length, results) 161 print("{:>25} |{:7.1f} ± {:4.0f} ({:5.0f} to {:5.0f}) |{:7.3f} secs/map | {} {}-city maps" 162 .format(tsp.__name__, mean(lengths), stddev(lengths), min(lengths), max(lengths), 163 time, len(maps), len(maps[0]))) 164 165 def mean(numbers): 166 return sum(numbers) / len(numbers) 167 168 def stddev(numbers): 169 """ 170 标准差 171 :param numbers: 172 :return: 173 """ 174 return (mean([x ** 2 for x in numbers]) - mean(numbers) ** 2) ** 0.5 175 176 """ 177 当城市的数量为多少时,nn_tsp能取得最好的效果 178 """ 179 def repeat_10_nn_tsp(cities):return repeated_nn_tsp(cities, 10) 180 def repeat_25_nn_tsp(cities):return repeated_nn_tsp(cities, 25) 181 def repeat_50_nn_tsp(cities):return repeated_nn_tsp(cities, 50) 182 def repeat_100_nn_tsp(cities):return repeated_nn_tsp(cities, 100) 183 184 algorithms = [nn_tsp, repeat_10_nn_tsp, repeat_25_nn_tsp, repeat_25_nn_tsp, 185 repeat_50_nn_tsp, repeat_100_nn_tsp] 186 print(benchmarks(algorithms)) 187 188 """ 189 最近邻面临的问题:离群点 190 """ 191 outliers_list = [City(2, 2), City(2, 3), City(2, 4), City(2, 5), City(2, 6), 192 City(3, 6), City(4, 6), City(5, 6), City(6, 6), 193 City(6, 5), City(6, 4), City(6, 3), City(6, 2), 194 City(5, 2), City(4, 2), City(3, 2), 195 City(1, 6.8), City(7.8, 6.4), City(7, 1.2), City(0.2, 2.8)] 196 197 outliers = set(outliers_list) 198 199 plot_lines(outliers, ‘bo‘)

1 plot_tsp(nn_tsp, outliers)
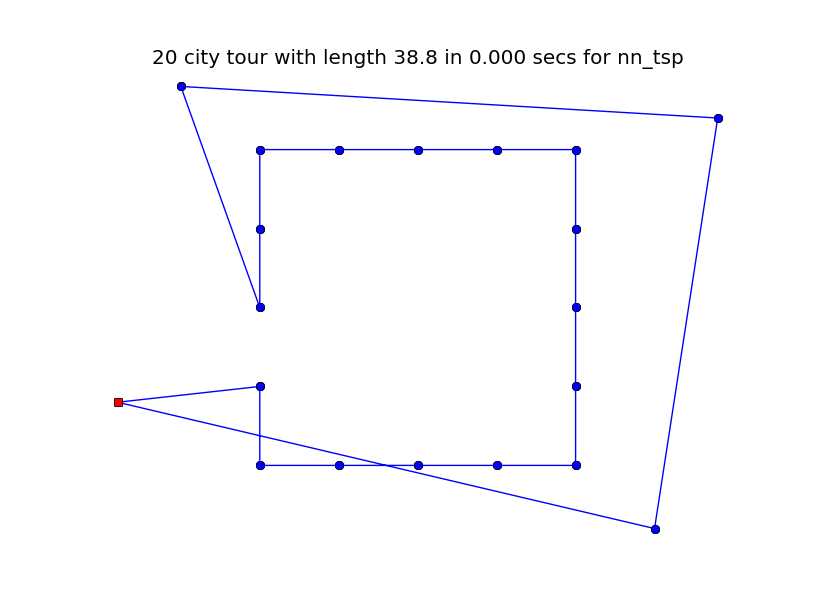
1 """ 2 存在四个围绕的离群点,但是我们却让它们各自连接————使用了最长的四条线 3 —————这不科学 4 """ 5 def plot_labeled_lines(points, *args): 6 """ 7 分别画出每个点并标记 8 :param points: 9 :param args: 10 :return: 11 """ 12 plot_lines(points, ‘bo‘) 13 for (label, p) in enumerate(points): 14 plt.text(X(p), Y(p), ‘ ‘+str(label)) 15 16 style = ‘bo-‘ 17 for arg in args: 18 if isinstance(arg, str): 19 style = arg 20 else:# arg 是points序列链 21 Xs = [X(points[i]) for i in arg] 22 Ys = [Y(points[i]) for i in arg] 23 plt.plot(Xs, Ys, style) 24 plt.axis(‘scaled‘) 25 plt.axis(‘off‘) 26 plt.show() 27 """ 28 注意到在第四个点时 29 """ 30 plot_labeled_lines(outliers_list, ‘bo-‘, [0, 1, 2, 3, 4], ‘ro--‘, [4, 16], ‘bo--‘, [4, 5])
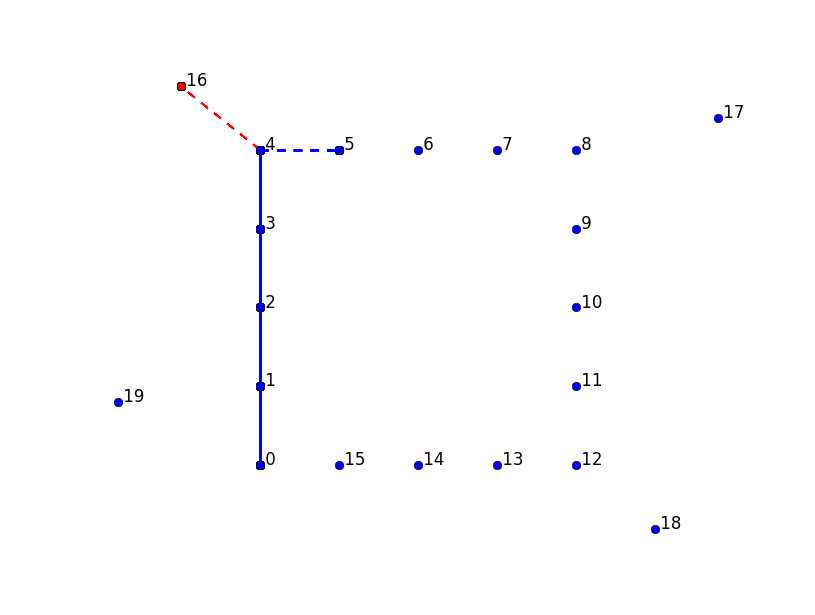
""" 此时若是选择离群点所得到的结果更优, 在没有模糊的环境下,很难决定是否选择离群点还是义无反顾的选择最近邻 建议在构建路径的过程中不要总是想着去做决定,不妨等到路径建设完全后再来考虑离群点 """
原文:http://www.cnblogs.com/kalpan/p/4364280.html