法线的变换矩阵

一、法线和顶点坐标的区别

顶点坐标<x,y,z>表示缺省的<x,y,z,1>，而法线向量的<x,y,z>表示缺省的<x,y,z,0>。

法线向量只能保证方向的一致性，而不能保证位置的一致性。 

下面我们通过一个例子来看看问题所在。

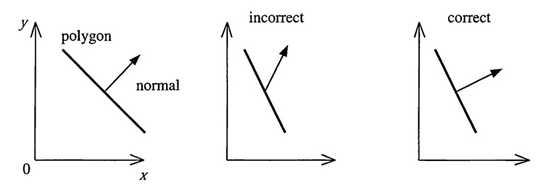
上图是针对一个多边形以及一条边上的法线进行缩放变换：X轴上缩放为原来的0.5倍。左边是变换前的状态，中间是将同样的模型变换矩阵应用在法线上的结果，显然是错的，法线并不垂直于切线。最右边的图是正确的结果。

二、法线变换：应该用变换矩阵的逆转置矩阵

假设Model space中的某条切线向量是T，法线向量是N。那么由他们是垂直的可得到：T^T?N=0

假设他们变换到Eye space中后分别是T‘和N‘。那么他们应该仍然是相互垂直的：T’^T?N’=0

假设切线向量和法线向量的变换矩阵为M(已知)、G(未知)。则有：

T’^T?N’ = 0   ==>   (MT)^T(GN) = T^TM^TGN = 0

由于T^TN=0，因此M^TG=E是上式的一个解. 此时，

G=(M^-1)^T

即：应用于法线向量的变换矩阵是顶点变换矩阵的逆转置矩阵。

法线的变换矩阵

原文：http://www.cnblogs.com/zjw0901/p/4364650.html