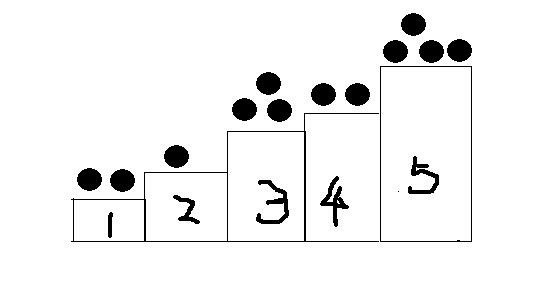

这个游戏可以转化为Nim游戏,石子堆所有 为排奇数位置的人与它后面一个排偶数位置人的距离
如果,石子堆为 a与b之间的距离1,c与d之间的距离1, 1^1=0,所以先手必败
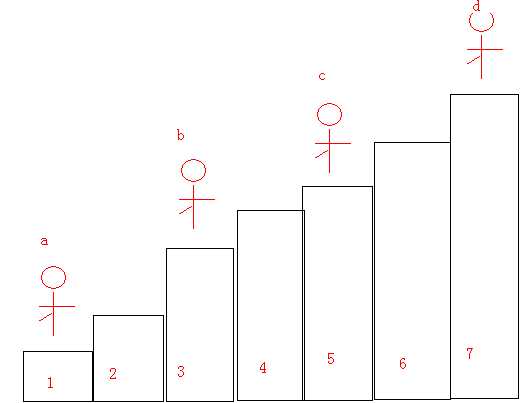
如图,无论排偶数位置的人怎么移动,排在它前面位置的人都能够跟着移动,但是排奇数位置的人移动,偶数位置的人就不能跟着移动
比如b向上移动一个台阶,那么a也能够向上一个台阶。那么总的局面还是 1^1.
1 #include <stdio.h> 2 #include <string.h> 3 const int N = 100 + 10; 4 int a[N],b[N]; 5 int main() 6 { 7 int n = 0,i,j,k,sum = 0; 8 while(scanf("%d",&a[n])!=EOF) 9 n++; 10 for(i=1; i<n; ++i) 11 b[i-1] = a[i] - a[i-1] - 1; 12 for(i=0; i<n-1; i+=2) 13 sum ^= b[i]; 14 if(sum==0) 15 printf("-1\n"); 16 else 17 { 18 //枚举第i个人移动j步,使得剩下的局面异或等于0, 19 for(i=0; i<n-1; ++i) 20 for(j=1; a[i]+j<a[i+1]; ++j) 21 { 22 23 b[i] -= j; 24 if(i!=0) 25 b[i-1] += j; 26 27 sum = 0; 28 for(k=0; k<n-1; k+=2) 29 sum ^= b[k]; 30 if(sum==0) 31 { 32 printf("%d %d\n",a[i],a[i]+j); 33 break; 34 } 35 b[i] += j; 36 if(i!=0) 37 b[i-1] -= j; 38 39 } 40 } 41 return 0; 42 }
原文:http://www.cnblogs.com/justPassBy/p/4367904.html