方法一:位图法,原理是首先申请一个长度为n且均为’0’组成的字符串,字符串的下标即为数组a[]中的元素,然后从头开始遍历数组a[N],取每个数组元素的值,将其对应的字符串中的对应位置置1,如果已经置过1,那么该数就是重复的数。由于采用的是位图法,所以空间复杂度比较大,为O(N).
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 |
#include "stdafx.h"#include <stdio.h>#include <stdlib.h>bool
xor_findDup(int
* arr, int
NUM){ int
*arrayflag = (int
*)malloc(NUM*sizeof(int)); int
i = 1; while
(i < NUM) { arrayflag[i] = false; i++; } for
(i = 0; i < NUM; i++) { if
(arrayflag[arr[i]] == false) { arrayflag[arr[i]] = true; } else return
true; }}int
main(){ int
a[] = {1,7,4,2,1,4,3,1}; if
(xor_findDup(a, 8)) printf("存在重复元素"); else printf("不存在重复元素"); getchar(); return
0;} |
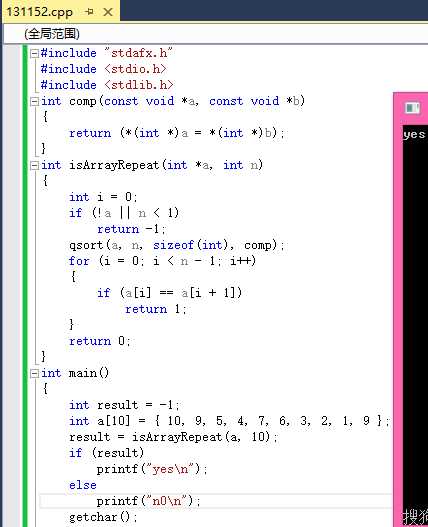
方法二:对数组进行排序,然后比较相邻的元素是否相同。C++标准库提供了快速排序的方法qsort(),可以直接用的。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 |
#include "stdafx.h"#include <stdio.h>#include <stdlib.h>int comp(const
void *a, const
void *b){ return
(*(int
*)a = *(int
*)b);}int isArrayRepeat(int
*a, int
n){ int
i = 0; if
(!a || n < 1) return
-1; qsort(a, n, sizeof(int), comp); for
(i = 0; i < n - 1; i++) { if
(a[i] == a[i + 1]) return
1; } return
0;}int
main(){ int
result = -1; int
a[10] = { 10, 9, 5, 4, 7, 6, 3, 2, 1, 9 }; result = isArrayRepeat(a, 10); if
(result) printf("yes\n"); else printf("n0\n"); getchar(); return
0;} |
效果如图:
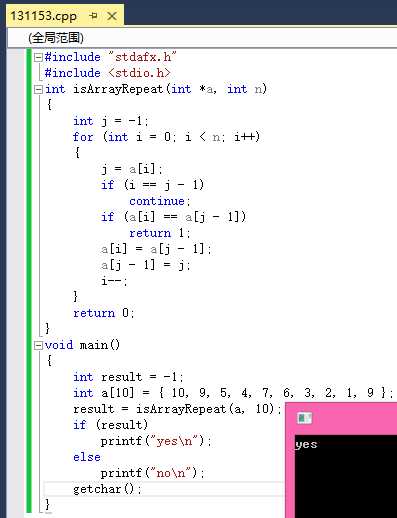
方法三:遍历数组,假设第i个位置的数字为i,则j的范围为1~n。通过交换将j换到下表为j-1的位置上。直到所有数字都出现在自己对应的下标处,或发生了冲突,即该位置已经被占。此时的时间复杂度为O(n)。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 |
#include "stdafx.h"#include <stdio.h>int isArrayRepeat(int
*a, int
n){ int
j = -1; for
(int i = 0; i < n; i++) { j = a[i]; if
(i == j - 1) continue; if
(a[i] == a[j - 1]) return
1; a[i] = a[j - 1]; a[j - 1] = j; i--; } return
0;}void
main(){ int
result = -1; int
a[10] = { 10, 9, 5, 4, 7, 6, 3, 2, 1, 9 }; result = isArrayRepeat(a, 10); if
(result) printf("yes\n"); else printf("no\n"); getchar();} |
效果如图:
假设数组a有n个元素,元素取值范围是1~n,如何判定数组是否存在重复元素,布布扣,bubuko.com
假设数组a有n个元素,元素取值范围是1~n,如何判定数组是否存在重复元素
原文:http://www.cnblogs.com/cysolo/p/3593029.html