【简介】
LCA(T,u,v):在有根树T中,询问一个距离根最远的结点x,使得x同时为结点u、v的祖先。
RMQ(A,i,j):对于线性序列A中,询问区间[i,j]上的最值。见我的博客---RMQ ---- ST(Sparse Table)算法。
【LCA算法】
解决LCA问题有多种算法,一种是离线的 Tarjan算法 ,还有在线的倍增法 ,还有就是转换为RMQ问题的在线算法。
【LCA转化为RMQ】
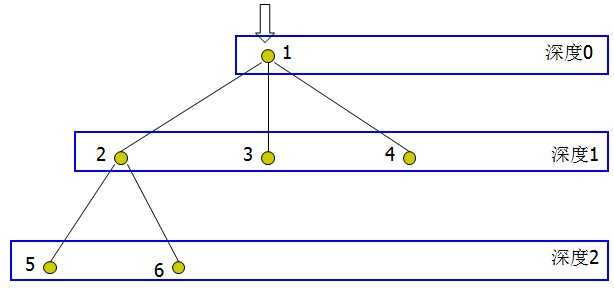
(一)对有根树T进行DFS,将遍历到的结点按照顺序记下,我们将得到一个长度为2N – 1的序列,称之为T的欧拉序列F 。
(二)每个结点都在欧拉序列中出现,我们记录结点u在欧拉序列中第一次出现的位置为pos(u)。

至此,LCA问题就转化为RMQ问题。
【RMQ转化为LCA】
简单说明下吧:考察一个长度为N的序列A,按照如下方法将其递归建立为一棵树:
最近公共祖先 Least Common Ancestors(LCA)算法 --- 与RMQ问题的转换
原文:http://www.cnblogs.com/wuminye/p/3525957.html