一直由于某些原因耽搁着...最小费用最大流没有搞会。
今天趁着个人状态正佳,赶紧去看看,果然30min不到看会了算法+模板并且A掉了一道题。
感觉最小费用最大流在学过了最大流之后还是挺好理解的。找到从起点到终点流过1单位流量的最小花费方案,然后更新数据。
不停地找增广路,不停累计答案,不停趋近最优解。
理解起来没有任何问题。代码书写一遍就过了很顺利。
POJ2135
实际上是一道并不那么容易套的模板题。
网络流的题目重在建模。这道题就是这样。
求起点到终点往返的最短路径,但不能经过相同的边。
往返一遍等同于从起点到终点走两遍。
乍一看觉得很像二取方格数,然后想到了最近A掉的K取方格数,就是用网络流算法。于是想到了网络流。
我们用流量为1来控制每条边只经过一次,然后增加一个源点和汇点,分别连0,n流量为2。
这样建模就建好啦!
但是刚刚想到了一个问题,来回两次的边都赋予了1的流量,这样不是可以来回各经过一次吗?
即这种情况。
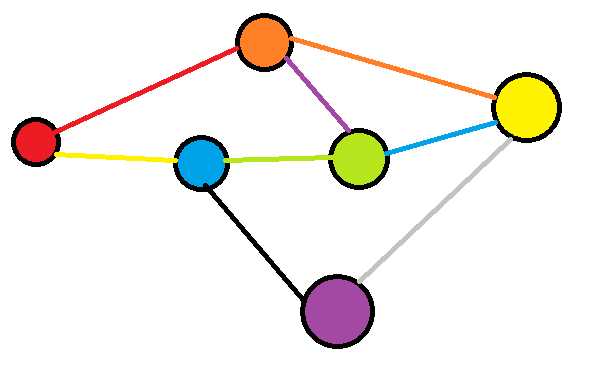
红-蓝-绿-黄是一条已经取好的路径。
当橙色边费用接近正无穷的时候,橙色点就会到绿-蓝-紫-黄
这样就经过了绿边两次。
但是很快发现这样的情况是不存在的。
完全可以取红-蓝-紫+红-橙-绿-黄,这样还减少了两条绿边的费用。题目中保证费用>0,所以这时我们可以发现这样的情况是不存在的。
于是代码就可以放心地敲起来啦!
(本来想再做几道最小费用最大流的题练练代码熟练度的,但由于时间比较紧...突然发现今天是周五,省选周一报到...本来印象中的还有三四天没想到是周末QAQ 然后得知明天下午还放假这样一来就根本没有
时间可以准备啦!所以鉴于这些原因...还是多留点时间给复习不熟练的东西吧)
program poj2135; const maxn=1010;maxm=50010; var n,m,i,j,x,y,z:longint; link,opt,dis,pre:array[-1..maxn]of longint; vis:array[-1..maxn]of boolean; fa,from,next,w,c,rev:array[-1..maxm]of longint; function min(a,b:longint):longint; begin if a<b then exit(a) else exit(b); end; procedure add(x,y,z,cc:longint); begin inc(j);fa[j]:=y;from[j]:=x;next[j]:=link[x];link[x]:=j;w[j]:=z;c[j]:=cc;rev[j]:=j+1; inc(j);fa[j]:=x;from[j]:=y;next[j]:=link[y];link[y]:=j;w[j]:=-z;c[j]:=0;rev[j]:=j-1; end; function spfa:boolean; var head,tail,x,j:longint; begin fillchar(dis,sizeof(dis),63); fillchar(vis,sizeof(vis),true); head:=0;tail:=1; opt[1]:=0;vis[0]:=false;dis[0]:=0; while head<>tail do begin head:=(head+1) mod maxn; x:=opt[head];j:=link[x]; while j<>0 do begin if (c[j]>0)and(dis[x]+w[j]<dis[fa[j]]) then begin dis[fa[j]]:=dis[x]+w[j]; pre[fa[j]]:=j; if vis[fa[j]] then begin tail:=(tail+1) mod maxn; opt[tail]:=fa[j]; end; end; j:=next[j]; end; vis[x]:=true; end; if dis[n+1]<>dis[-1] then exit(true) else exit(false); end; function MCMF:longint; var ans,x,sum:longint; begin ans:=0; while spfa do begin sum:=maxlongint; x:=n+1; while x<>0 do begin sum:=min(sum,c[pre[x]]); x:=from[pre[x]]; end; x:=n+1; while x<>0 do begin inc(ans,sum*w[pre[x]]); dec(c[pre[x]],sum); inc(c[rev[pre[x]]],sum); x:=from[pre[x]]; end; end; exit(ans); end; begin assign(input,‘poj2135.in‘);reset(input); readln(n,m);j:=0; for i:=1 to m do begin readln(x,y,z); add(x,y,z,1);add(y,x,z,1); end; add(0,1,0,2);add(n,n+1,0,2); writeln(MCMF); end.
原文:http://www.cnblogs.com/mjy0724/p/4372859.html