1 import java.util.Scanner; 2 public class Suan { 3 public static void main(String[] args) { 4 int []b;//设置数组来存放随机产生数 5 b=new int [4]; 6 Scanner in=new Scanner(System.in); 7 System.out.println("请选择你想练习的题型:"); 8 System.out.println(" 1、分数的加减乘数法练习!"); 9 System.out.println(" 2、整数的加减乘数法练习!"); 10 int xuanze=in.nextInt(); 11 System.out.println("你想输出四则运算的个数是:"); 12 int num=in.nextInt(); 13 String []a={"+","-","*","/"};//整数运算存放符号的数组 14 String res,res1 = null, sum1=null;//res为你输入的答案,res1为分数运算和整数运算除法中的正确答案 15 int []c;//符号的代数 16 int j=0,sum2=0;//sum2为整数运算中加减除的用户输入答案 17 int rshu = 0;//用户计算正确数 18 c=new int [4]; 19 if(1==xuanze)//选择应该输出怎样类型的算式 20 { 21 for(int i=0;i<4;i++)//产生符号的代数 22 { 23 c[i]=(int)(Math.random()*14/3); 24 } 25 for( j=0;j<num;j++)//不够num个数就继续输出算式 26 { 27 for(int i=0;i<4;i++)//产生1到10的随机数 28 { 29 b[i]=(int)( Math.random()*10); 30 } 31 32 if(b[0]>b[1]&&b[2]>b[3]&&b[0]!=0&&b[1]!=0&&b[2]!=0&&b[3]!=0)//真分数的前提 33 { 34 System.out.println("("+b[1]+"/"+b[0]+")"+ a[c[0]]+"("+ b[3]+"/"+b[2]+")"); 35 System.out.print("你的答案是:"); 36 res=in.next(); 37 switch(c[0]){//调用成员方法计算 38 case 0:res1=fracAdd(b[1],b[0],b[3],b[2]);break; 39 case 1:res1=fracSub(b[1],b[0],b[3],b[2]);break; 40 case 2:res1=fracMul(b[1],b[0],b[3],b[2]);break; 41 case 3:res1=fractDiv(b[1],b[0],b[3],b[2]);break; 42 } 43 if(!res.equals(res1))//比较答案 44 { 45 System.out.println("你的答案错误!正确答案为:"+res1); 46 } 47 else 48 { 49 rshu++;//用户计算正确数 50 } 51 } 52 else 53 j--; 54 } 55 } 56 if (2==xuanze)//选择整型数算式 57 { 58 59 for( int r=0;r<num;r++)//不够num个数就继续输出算式 60 { 61 int sum = -1;//真正的结果 62 for(int i=0;i<4;i++) 63 { 64 b[i]=(int)( Math.random()*100); 65 } 66 for(int i=0;i<4;i++) 67 { 68 c[i]=(int)(Math.random()*14/3); 69 } 70 switch(c[0])//判断应该用什么符号 71 { 72 case 0 : 73 case 1 :sum=b[0]+b[1];break; 74 case 2 :sum=b[0]-b[1];break; 75 case 3 :sum=b[0]*b[1];break; 76 case 4 : sum1=fractDiv2(b[0],b[1]);break;//除号时调用函数,结果显示分数 77 } 78 /*if(sum<0)//减法计算结果不能为0 79 { 80 j--; 81 }*/ 82 if(c[0]==4)//如果符号是除号时 83 { 84 System.out.println(b[0]+a[c[0]-1]+b[1]+"="); 85 System.out.print("你的答案是:"); 86 res=in.next(); 87 if(!res.equals(sum1)) 88 { 89 System.out.println("你的答案错误!正确答案为:"+sum1); 90 } 91 else 92 rshu++; 93 } 94 else//如果符号不是除号时 95 { 96 System.out.println(b[0]+a[c[0]-1]+b[1]+"="); 97 System.out.print("你的答案是:"); 98 sum2=in.nextInt(); 99 if(sum2!=sum) 100 { 101 System.out.println("你的答案错误!正确答案为:"+sum); 102 } 103 else 104 rshu++; 105 //System.out.println(sum); 106 } 107 System.out.println(r); 108 109 } 110 } 111 else 112 {} 113 System.out.println("你一共答对了"+rshu+"道题"); 114 115 } 116 static String fracAdd(int first_numerator,int first_denominator,int second_numrator,int second_denominator){ 117 //分数加法 118 //需要调用求最大公约数的函数 119 120 int denominator; //分子 121 int numerator; //分母 122 123 if(first_denominator==second_denominator) //分母相同时加分子 124 { 125 denominator=first_denominator; 126 numerator=first_numerator+second_numrator; 127 } 128 else //否则同分比较分子 129 { 130 denominator=first_denominator*second_denominator; 131 numerator=first_numerator*second_denominator+first_denominator*second_numrator; 132 } 133 int gcd = gcd(numerator,denominator); //调用gcd方法约分 134 denominator = denominator / gcd; 135 numerator = numerator / gcd; 136 if(0==denominator/numerator) 137 { 138 String res="0"; 139 return res; 140 } 141 else 142 { 143 String zi1=String.valueOf(numerator);//把结果转换成字符串输出 144 String zi2=String.valueOf(denominator);//把结果转换成字符串输出 145 String zi3="/";//把结果转换成字符串输出 146 String res2=zi1+zi3+zi2;//把结果转换成字符串输出 147 148 return res2; } 149 150 } 151 static String fracSub(int first_numerator,int first_denominator,int second_numrator,int second_denominator){ 152 153 //需要调用求最大公约数的函数 154 155 int denominator; 156 int numerator; 157 158 if(first_denominator==second_denominator) //分母相同时加分子 159 { 160 denominator=first_denominator; 161 numerator=first_numerator-second_numrator; 162 } 163 else //否则同分比较分子 164 { 165 denominator=first_denominator*second_denominator; 166 numerator=first_numerator*second_denominator-first_denominator*second_numrator; 167 } 168 int gcd = gcd(numerator,denominator); 169 denominator = denominator / gcd; 170 numerator = numerator / gcd; 171 if(0==denominator/numerator) 172 { 173 String res="0"; 174 return res; 175 } 176 else 177 { 178 String zi1=String.valueOf(numerator); 179 String zi2=String.valueOf(denominator); 180 String zi3="/"; 181 String res2=zi1+zi3+zi2; 182 return res2; } 183 184 } 185 static String fracMul(int first_numerator,int first_denominator,int second_numerator,int second_denominator){ 186 187 //需要调用求最大公约数的函数 188 int denominator; 189 int numerator; 190 191 192 denominator=first_denominator*second_denominator; 193 numerator=first_numerator*second_numerator; 194 195 int gcd = gcd(numerator,denominator); 196 denominator = denominator / gcd; 197 numerator = numerator / gcd; 198 if(0==denominator/numerator) 199 { 200 String res="0"; 201 return res; 202 } 203 else 204 { 205 String zi1=String.valueOf(numerator); 206 String zi2=String.valueOf(denominator); 207 String zi3="/"; 208 String res2=zi1+zi3+zi2; 209 return res2; } 210 211 } 212 static String fractDiv(int first_numerator,int first_denominator,int second_numerator,int second_denominator){ 213 214 //需要调用求最大公约数的函数 215 216 int denominator; 217 int numerator; 218 219 numerator = first_numerator*second_denominator; 220 denominator = first_denominator*second_numerator; 221 222 223 224 int gcd = gcd(numerator,denominator); 225 denominator = denominator / gcd; 226 numerator = numerator / gcd; 227 String zi1=String.valueOf(numerator); 228 String zi2=String.valueOf(denominator); 229 String zi3="/"; 230 String res2=zi1+zi3+zi2; 231 return res2; 232 233 } 234 static String fractDiv2(int first,int second){ 235 236 //需要调用求最大公约数的函数 237 int denominator= first; 238 int numerator= second; 239 int gcd = gcd(numerator,denominator); 240 denominator = denominator / gcd; 241 numerator = numerator / gcd; 242 String zi1=String.valueOf(numerator); 243 String zi2=String.valueOf(denominator); 244 String zi3="/"; 245 String res2=zi1+zi3+zi2; 246 return res2; 247 } 248 static int gcd(int x,int y){ //利用辗转相除法求最大公约数 249 int r; 250 while( y!= 0) 251 { 252 r = x%y; 253 x = y; 254 y = r; 255 } 256 return x; 257 258 } 259 260 261 }
运行结果:
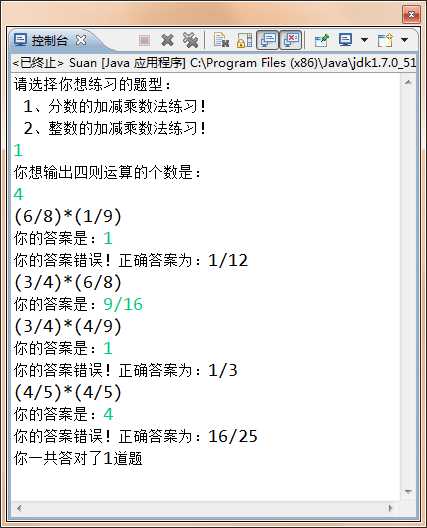
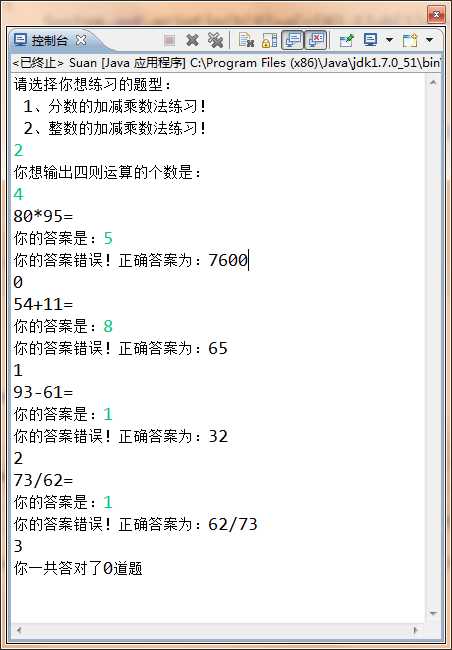
感想:用了四个小时左右把原来的那个作业一修改成可以自动生成分数加减乘除的算法,虽然还不太完善,但是,基本功能还是实现了。感觉很开心
注:昨天下午已经把程序写好,只是学校网络一直上传不了程序,今天没办法,只能用手机开WiFi电脑连然后发布!T_T
原文:http://www.cnblogs.com/Lingchao/p/4373569.html