URAL 1507. Difficult Decision（矩阵快速幂）

题目链接：http://acm.timus.ru/problem.aspx?space=1&num=1507

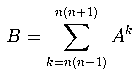
Input

Output

Samples

2
0 7
15 30

Yes

3
100 35 40
0 22 0
10 11 0

No

PS:

正解是用bool把相乘的结果中不为零的用true代替，不然会爆！

#include<stdio.h>
#include<string.h>

struct Matrix
{
    int m[51][51];
};
struct Matrix I,s;
int n,kmod;

Matrix Mul(Matrix a,Matrix b)
{
    Matrix c;
    int i,j,k;
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            c.m[i][j]=0;
            for(k=0; k<n; k++)
            {
                c.m[i][j]+=(a.m[i][k]*b.m[k][j]);
            }
            if(c.m[i][j]>0) c.m[i][j]=1;
            else c.m[i][j]=0;
        }
    }
    return c;
}

Matrix Add(Matrix a,Matrix b)
{
    Matrix c;
    int i,j;
    for(i=0; i<n; i++)
    {
        for(j=0; j<n; j++)
        {
            c.m[i][j]=(a.m[i][j]+b.m[i][j]);
            if(c.m[i][j]>0) c.m[i][j]=1;
            else c.m[i][j]=0;
        }

    }
    return c;
}

Matrix Quickpow(Matrix a,int n)
{
    Matrix m,b;
    m=a,b=I;
    while(n)
    {
        if(n%2)
            b=Mul(b,m);
        n/=2;
        m=Mul(m,m);
    }
    return b;
}


int main()
{
    int i,j;
    int k;
    while(scanf("%d",&n)!=EOF)
    {
        Matrix ans;
        memset(I.m,0,sizeof I.m);
        memset(ans.m,0,sizeof ans.m);
        for(i=0; i<n; i++)
            I.m[i][i]=1;
        for(i=0; i<n; i++)
        {
            for(j=0; j<n; j++)
            {
                scanf("%d",&s.m[i][j]);
                if(s.m[i][j]>0) s.m[i][j]=1;
                else s.m[i][j]=0;
            }
        }

        for(i=n*(n-1); i<=n*(n+1); i++)
            ans=Add(ans,Quickpow(s,i));
        int flag=1;
        for(i=0; i<n; i++)
        {
            for(j=0; j<n; j++)
            {
                if(ans.m[i][j]==0)
                    flag=0;
            }
        }
        if(flag) puts("Yes");
        else puts("No");
    }

    return 0;
}

URAL 1507. Difficult Decision（矩阵快速幂）

原文：http://blog.csdn.net/u012860063/article/details/44698643