ural 1507 Difficult Decision

H - Difficult Decision

Time Limit:1000MS     Memory Limit:65536KB     64bit IO Format:%I64d & %I64u

Submit Status Practice URAL 1507

Description

Often, when a decision about investing in a new business must be taken, a New Russian has to estimate quickly whether a certain project will be a success or not. Leading economists have recently discovered a new algorithm for forecasting the success of a project.

First, one has to form an n × n matrix of risks. Let us denote this matrix by A. Then, in order to take into account the interdependencies of the parameters inside the matrix, the matrix

must be computed. If at least one of the elements of the matrix B is zero, then there is a considerable probability that the project will fail. Otherwise, if there are no zero elements in the matrix B, the new business will grow and flourish.

Help New Russians to make use of this algorithm. Your task is to write a program that determines the probability of the success of a project given the matrix of its risks.

Input

The first line of the input contains the dimension n of the matrix A (2 ≤ n ≤ 50). Each of the next n lines contains n numbers that forms the matrix A. Each element is a whole number in the range from 0 to 100.

Output

Output "No" if there is at least one zero element in the matrix B (so it is better not to invest in the new business). Otherwise, output "Yes".

Sample Input

input	output
2 0 7 15 30	Yes
3 100 35 40 0 22 0 10 11 0	No

被坑了两个小时。。。

题意：一个矩阵B等于矩阵A。（）。。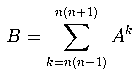

对A的K次方（K有范围）求和。。

给定一个n*n的矩阵A。问你求出的B矩阵是否存在0.

有0就NO

否则就YES。

第一想法是直接矩阵快速幂暴力求解。。

后来T 了。一直纠结了两个小时。。。

最后才知道矩阵要用bool 定义。。

不然k太大的话乘法必然会溢出。。

#include <stdio.h>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
using namespace std;
__int64 n;
struct node
{
    bool a[55][55];   //bool 类型的矩阵，值只有0和一。。
};
node mut_mut(node e,node d) //两个矩阵相乘
{
    __int64 i,j,k;
    node m;
    memset(m.a,0,sizeof(m.a));
    for(i=1; i<=n; i++)
        for(j=1; j<=n; j++)
            for(k=1; k<=n; k++)
                m.a[i][j]+=e.a[i][k]*d.a[k][j];
    return m;
}
node fastmi(node a1,__int64 cishu)  //快速幂
{
    __int64 i;
    node f;
    memset(f.a,0,sizeof(f.a));
    for(i=1; i<=n; i++)
        f.a[i][i]=1;   //初始化单位矩阵。
    while(cishu)
    {
        if(cishu&1)
            f=mut_mut(f,a1);
        a1=mut_mut(a1,a1);
        cishu>>=1;
    }
    return f;
}
node xiangjia(node c,node b) //相加。。
{
    __int64 i,j;
    node u;
    memset(u.a,0,sizeof(u.a));
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=n; j++)
        {
            if(c.a[i][j]==0 &&b.a[i][j]==0)
                continue;
            u.a[i][j]+=c.a[i][j]+b.a[i][j];
        }
    }
    return u;
}
int main()
{
    __int64 i,j,p,l;
    node c,last,v,t;
    while(~scanf("%I64d",&n))
    {
        int flag=1;
        for(i=1; i<=n; i++)
            for(j=1; j<=n; j++)
                scanf("%I64d",&c.a[i][j]);
        i=n*(n-1);
        l=n*(n+1);
        memset(t.a,0,sizeof(t.a));
        for(p=i; p<=l; p++)
        {
            v=fastmi(c,p);   
            t=xiangjia(t,v);      //直接在k的范围内暴力出矩阵B。
        }
        for(i=1; i<=n; i++)
        {
            for(j=1; j<=n; j++)
            {
                cout<<t.a[i][j]<<" ";
                if(t.a[i][j]==0)
                {
                    flag=0;
                    break;
                }
            }
            if(!flag)
                break;
        }
        if(!flag)
            printf("No\n");
        else
            printf("Yes\n");
        memset(t.a,0,sizeof(t.a));
    }
    return 0;
}

ural 1507 Difficult Decision

原文：http://blog.csdn.net/sky_miange/article/details/44698483