题目:返回一个整数数组中最大子数组的和。
要求:
(1)输入一个整形数组,数组里有正数也有负数。
(2)数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
(3)如果数组A[0]……A[j-1]首尾相邻,允许A[i-1], …… A[n-1], A[0]……A[j-1]之和最大。
(4)同时返回最大子数组的位置。
(5)求所有子数组的和的最大值。要求时间复杂度为O(n)。
一、设计思想
这个问题的最优解一定是以下两种可能。
可能一:最优解没有跨过array[n-1]到array[0],即和非环形数组一样了。
可能二:最优解跨过array[n-1]到array[0],新问题。
对于第一种情况,我们可以按照非环形数组求法来求,为max1;对于第二种情况,可以将原问题转化为数组的最小子数组和问题,再用数组全部元素的和减去最小子数组和,那么结果一定是跨过a[n-1]到a[0]情况中最大的子数组和,设为max2。最终结果即为max1与max2中较大的那个。
例1:有数组5、-1、-6、8、2
求得max1=10,max2=15,则取较大的max2作为结果。
例2:有数组-6、8、1、6、-1
求得max1=15,max2=14,则取较大的max1作为结果。
二、源程序
1 package com.java.lianxi; 2 import java.util.*; 3 public class lianxi3 { 4 public static void main(String[] args) 5 { 6 int num,i; 7 int sum=0; 8 int max; 9 Scanner cin=new Scanner(System.in); 10 System.out.print("请输入数组的长度:"); 11 num=cin.nextInt(); 12 int array[]=new int[num]; 13 int max1=array[0]; 14 int min=array[0]; 15 for(i=0;i<num;i++) 16 { 17 array[i]=cin.nextInt(); 18 } 19 for(i=0;i<num;i++) 20 { 21 if(sum<=0) 22 { 23 sum=array[i]; 24 } 25 else 26 { 27 sum=sum+array[i]; 28 } 29 if(sum>max1) 30 { 31 max1=sum; 32 } 33 } 34 System.out.println("第一种情况的最大值:"+max1); 35 for(i=0;i<num;i++) 36 { 37 if(sum>=0) 38 { 39 sum=array[i]; 40 41 } 42 else 43 { 44 sum=sum+array[i]; 45 46 } 47 if(sum<min) 48 { 49 min=sum; 50 } 51 } 52 int sum1=0; 53 for(i=0;i<num;i++) 54 { 55 sum1=sum1+array[i]; 56 } 57 int max2=sum1-min; 58 System.out.println("第二种情况的最大值:"+max2); 59 if(max1>max2) 60 { 61 max=max1; 62 } 63 else 64 { 65 max=max2; 66 } 67 System.out.println("子数组和的最大值为:"+max); 68 } 69 70 }
三、运行结果截图:

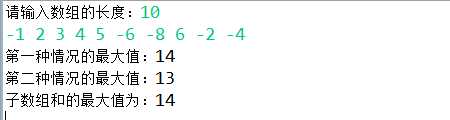
四、心得体会
首先是设计思路,一开始我们在课上和同学们想的也都差不多,就是单纯求最大子数组的和,后来我们在写程序过程中,时间复杂度不符合要求,新增了一种思路,即求“sum - 最小子数组和“。两种情况的最大字数组的和都和之前那种非环形的数组求和思路一样,实现起来比重构数组神马的简单些,现在还没有实现返回子数组,.。。。。。。
原文:http://www.cnblogs.com/maximumminimum/p/4374102.html