二叉树高度，以及栈实现二叉树的先序，中序，后序遍历的非递归操作

求解二叉树的高度

树是递归定义的，所以用递归算法去求一棵二叉树的高度很方便。

#include <iostream>  
#include <cstdio>  
using namespace std;  
  
struct Node {  
    char data;  
    Node *lchild;  
    Node *rchild;  
};  
  
void High(Node *T, int &h)  
{  
    if (T == NULL)  
        h = 0;  
    else {  
        int left_h;  
        High(T->lchild, left_h);  
        int right_h;  
        High(T->rchild, right_h);  
  
        h = 1 + max(left_h, right_h);  
    }  
}  
  
Node *CreateBiTree(Node *&T) {  // 算法6.4  
    // 按先序次序输入二叉树中结点的值（一个字符），空格字符表示空树，  
    // 构造二叉链表表示的二叉树T。  
    char ch;  
    cin >> ch;  
    if (ch == '#')  
        T = NULL;  
    else {  
        if (!(T = (Node *)malloc(sizeof(Node))))  
            return 0;  
        T->data = ch;              // 生成根结点  
        CreateBiTree(T->lchild);   // 构造左子树  
        CreateBiTree(T->rchild);   // 构造右子树  
    }  
    return T;  
} // CreateBiTree  
  
void Free(Node *&T)  
{  
    if (T == NULL)  
        return;  
  
    Free(T->lchild);  
    //  T->lchild = NULL;  
    Free(T->rchild);  
    //  T->rchild = NULL;  
    free(T);  
    T = NULL;  
}  
  
int main(int argc, char **argv)  
{  
    freopen("cin.txt", "r", stdin);  
  
    Node *T = NULL;  
    CreateBiTree(T);  
  
    int height;  
    High(T, height);  
    cout << height << endl;  
  
    Free(T);  
  
    return 0;  
}  
  
/* cin.txt: 
A 
B 
C 
# 
# 
D 
E 
# 
G 
# 
# 
F 
# 
# 
# 
*/  

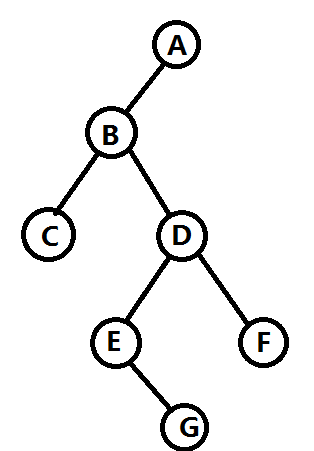
构造的树：

输出为5。

栈实现二叉树的先序，中序，后序遍历的非递归操作

中序遍历

void inOrder(BiTree T,void(*vist)( element e)){
     stack<Bitree> S;
     while (true){
           if (T) { s.push(T);T=T->Lchild;}
           else {T=s.top(); visit(T);s.pop();T=T->Rchild;}
           if(s.empty()&&T==NULL) break;
     }
}

void inOrder(BiTree T,void(*vist)( element e)){
            stack<Bitree> S;
            while(true){
            if(T){  visit(T);
                    if(T->rChild) s.push(T->rChild);T=T->lChild;}
            else {T=s.top();s.pop();}
            if (s.empty()&&T==NULL) break; }
}

void inOrder(BiTree T,void(*vist)( element e)){  
            stack<Bitree> S;  
            int flat[20];  
            while(true){  
                 while(true){  
                   s.push(T);T=T->lChild; flag(s.size()]=0;  
                   if (!T){ T=->rChild; if (T) flag[s.size()]=1; else break;}  
                   while (true){ if(flag[s.size()]){ T=s.top(); visit(T); s.pop();}  
                   else T=T->rChild;  
                }  
                if (s.empty()&&T==NULL) break;  
           }  
}

这三种方案都属于深度优先，还有广度优先的遍历，利用队列解决。

利用栈实现二叉树的先序，中序，后序遍历的非递归操作，

    #include <stdio.h>  
    #include <malloc.h>  
    #include <stdlib.h>  
    #include <queue>  
    #include <stack>  
    #include <iostream>  
    using namespace std;  
    typedef struct BiTNode{  
        char data;  
        BiTNode *lchild, *rchild;  
    }BiTNode,*BiTree;  
      
    void CreateBiTree(BiTree &T)//建树，按先序顺序输入节点  
    {  
        char ch;  
        scanf("%c",&ch);  
        if(ch==' ')  
        {  
            T=NULL;  
            return;  
        }  
        else  
        {  
            T=(BiTree)malloc(sizeof(BiTNode));  
            if(!T)  
                exit(1);  
            T->data=ch;  
            CreateBiTree(T->lchild);  
            CreateBiTree(T->rchild);  
        }  
    }  
    void InOrderTraverse(BiTree T)//非递归中序遍历  
    {  
          
        stack<BiTree> Stack;  
        if(!T)  
        {  
            printf("空树！\n");  
            return;  
        }  
          
        while(T || !Stack.empty())  
        {  
            while(T)  
            {  
                Stack.push(T);  
                T=T->lchild;  
            }  
            T=Stack.top();  
            Stack.pop();  
            printf("%c",T->data);  
            T=T->rchild;  
        }                                                                                                                                     
    }  
      
      
      
    void PreOrderTraverse(BiTree T)//非递归先序遍历  
    {  
          
        stack<BiTree> Stack;  
        if(!T)  
        {  
            printf("空树！\n");  
            return;  
        }  
        while(T || !Stack.empty())  
        {  
            while(T)  
            {  
                Stack.push(T);  
                printf("%c",T->data);  
                T=T->lchild;  
            }  
            T=Stack.top();  
            Stack.pop();          
                 T=T->rchild;          
        }                                                                                                                                     
    }  
      
      
    void PostOrderTraverse(BiTree T)//非递归后序遍历,用一个标记标记右子树是否访问过  
    {  
        int flag[20];  
        stack<BiTree> Stack;  
        if(!T)  
        {  
            printf("空树！\n");  
            return;  
        }  
        while(T)  
        {  
            Stack.push(T);  
            flag[Stack.size()]=0;  
            T=T->lchild;  
        }  
        while(!Stack.empty())  
        {  
            T=Stack.top();            
            while(T->rchild && flag[Stack.size()]==0)  
            {  
                flag[Stack.size()]=1;  
                T=T->rchild;  
                while(T)  
                {  
                    Stack.push(T);  
                    flag[Stack.size()]=0;  
                    T=T->lchild;  
                }  
            }  
            T=Stack.top();  
            printf("%c",T->data);  
            Stack.pop();  
        }                                                                                                                                     
    }  
    void main()  
    {  
        
        BiTree T;  
        CreateBiTree(T);  
        PreOrderTraverse(T);  
        printf("\n");  
             InOrderTraverse(T);  
        printf("\n");  
        PostOrderTraverse(T);  
        printf("\n");  
    }  

二叉树高度，以及栈实现二叉树的先序，中序，后序遍历的非递归操作

原文：http://blog.csdn.net/txl199106/article/details/44731371