一、题目与要求
题目:返回一个整数数组中最大子数组的和。
要求:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
如果数组A[0]……A[j-1]首尾相邻,允许A[i-1], …… A[n-1], A[0]……A[j-1]之和最大。
同时返回最大子数组的位置。
求所有子数组的和的最大值。要求时间复杂度为O(n)
二、设计思路
1、在上一次求一维数组最大子数组的问题上,进行拓展,继续使用类似的求和方法
2、应题目要求,这次的一位数组要首尾相连,允许A[i-1], …… A[n-1], A[0]……A[j-1]之和最大,所以我们采用课上的方法寻找最大值,将数组的元素进行扩展,即把数组除最后一个元素外从新拼接到尾部,形成一个环。
三、源代码
#include <iostream.h>
#define N 1000
int main(int argc, char* argv[])
{
int arry[N];
int length;
int max[N],max1;
int maxweizhi[N];
int value( int arry[],int length);
cout<<"请输入要比较整数的个数:"<<endl;
cin>>length;
cout<<"请输入整数"<<endl;
for(int i=0;i<length;i++)
{
cin>>arry[i];
}
int num=0;
for(int j=length;j<2*length-1;j++)
{
arry[j]=arry[num];
num++;
}
cout<<"由这几个数形成的环形数组";
value(arry,2*length-1);
return 0;
}
int value( int arry[],int length)
{
int max[N],max1;
int maxweizhi[N];
for(int j=0;j<(length+1)/2;j++)
{
int sum=0;
max1=-9999999;
int z=0;
for(int i=j;i<(length+1)/2+j;i++)
{
sum=sum+arry[i];
if(sum>=max1)
{
max1=sum;
z++;
}
}
max[j]=max1;
maxweizhi[j]=z;
}
int fmax=max[0];
int q=0;
for(int i=0;i<(length+1/2);i++)
{
if(max[i]>fmax)
{
fmax=max[i];
q=i;
}
}
int weizhi=maxweizhi[q];
cout<<"最大子数组为:"<<endl;
for(int num=q;num<q+weizhi;num++)
{
cout<<arry[num];
}
cout<<"其和为: "<<fmax<<endl;
return 0;
}
四、运行结果
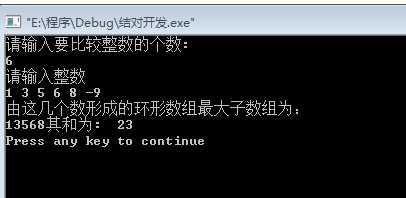
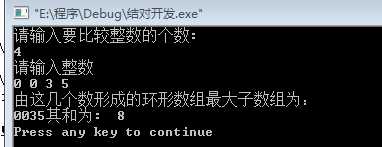
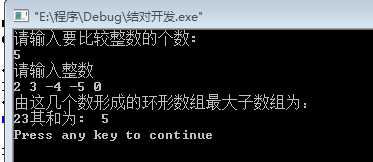
五、总结
通过此次实验,我认识到团结的力量。刚开始,我和小伙伴都没有思路,在课堂上,经过同学和老师的启发,对求解方法有了思路。这也让我们在课下编程
省了不少功夫。通过这次实验,也反思自己存在的问题。别人可以想出简单的方法,我们想不出来的原因在于练习的少,遇到和解决问题的机会也少。所以,还
是需要多多练习。每次解决问题后,都应该及时的反思总结,将方法求解归总,不断积累。
原文:http://www.cnblogs.com/yuji5656/p/4376594.html